题目内容
16.从-2、-1、0、2、5这一个数中,随机抽取一个数记为m,若数m使关于x的不等式组$\left\{\begin{array}{l}{x>m+2}\\{-2x-1≥4m+1}\end{array}\right.$无解,且使关于x的分式方程$\frac{x}{x-2}$+$\frac{m-2}{2-x}$=-1有非负整数解,那么这一个数中所有满足条件的m的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 不等式组整理后,根据无解确定出m的范围,进而得到m的值,分式方程去分母后将m的值代入检验,使分式方程的解为非负整数即可.
解答 解:不等式组整理得:$\left\{\begin{array}{l}{x>m+2}\\{x≤-2m-1}\end{array}\right.$,
由不等式组无解,得到m+2≥-2m-1,
解得:m≥-1,即m=-1,0,2,5,
分式方程去分母得:x-m+2=-x+2,即x=$\frac{1}{2}$m,
把m=-1代入得:x=-$\frac{1}{2}$,不符合题意;
把m=0代入得:x=0,符合题意;
把m=2代入得:x=1,符合题意;
把m=5代入得:x=2.5,不符合题意,
则所有满足条件m的个数是2,
故选B
点评 此题考查了分式方程的解,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
12.有下列四个命题:①相等的角是对顶角;②同位角相等;③若一个角的两边与另一个角的两边互相平行,则这两个角一定相等;④从直线外一点到这条直线的垂线段,叫做点到直线的距离.其中是真命题的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
4.有理数-3的绝对值是( )
| A. | 3 | B. | -3 | C. | ±3 | D. | $\sqrt{3}$ |
11.要使分式$\frac{x-3}{2-x}$有意义,则x的取值应满足( )
| A. | x≠3 | B. | x≠2 | C. | x<2 | D. | x>2 |
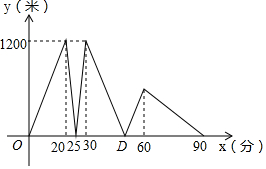 某景区的三个景点A、B、C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C;乙在甲出发20分钟后乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C:甲、乙两人同时到达景点C,甲、乙两人之间的距离y(米)与甲出发的时间x(分)之间的函数图象如图所示.
某景区的三个景点A、B、C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C;乙在甲出发20分钟后乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C:甲、乙两人同时到达景点C,甲、乙两人之间的距离y(米)与甲出发的时间x(分)之间的函数图象如图所示. 如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C(0,4),顶点为(1,$\frac{9}{2}$).
如图,在平面直角坐标系中,抛物线与x轴交于A、B两点(A在B的左侧),与y轴交于点C(0,4),顶点为(1,$\frac{9}{2}$).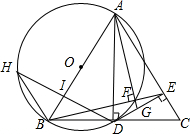 如图,在△ABC中,AB=AC,AD⊥BC,DE⊥AC,△ABD的外接圆交BE于F,连接AF,并延长AF交DE于G.
如图,在△ABC中,AB=AC,AD⊥BC,DE⊥AC,△ABD的外接圆交BE于F,连接AF,并延长AF交DE于G.