题目内容
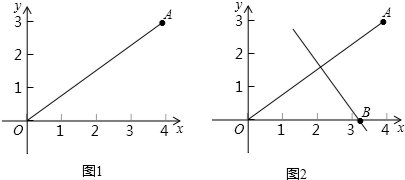
 2014年6月2日,富顺县一运动协会在县内的沱江河进行了一次划船比赛;参赛的船只在县城的晨光大桥下的沱江河面平行排开,并在上午9时同时出发,其中甲、乙两队在比赛时的路程y(千米)与时间x(小时)的函数关系如图所示,甲队在上午11时30分到达终点站千年古镇赵化的正码头.
2014年6月2日,富顺县一运动协会在县内的沱江河进行了一次划船比赛;参赛的船只在县城的晨光大桥下的沱江河面平行排开,并在上午9时同时出发,其中甲、乙两队在比赛时的路程y(千米)与时间x(小时)的函数关系如图所示,甲队在上午11时30分到达终点站千年古镇赵化的正码头.(1)哪个队先到达终点?到达的时间是多少?乙何时追上甲队?
(2)在比赛过程中,甲、乙何时相距最远?
考点:一次函数的应用
专题:
分析:(1)甲队在上午11时30分到达终点,共花时间2.5小时,从图象上看,AB线是甲队的路程,所以是乙队花时间少,先到终点.从图象来看,乙队的路程与时间成正比例关系,甲队的路程与时间是一个分段函数,即在1小时内是正比例函数,在1到2.5小时是一次函数,可使用待定系数法分别求出.乙队追上甲队时,两队的路程相等,列出方程可求解;
(2)由图看出1小时之内,两队相距最远距离是4千米;乙队追上甲队后,两队的距离也可计算,相比较得出甲、乙两队在出发后1小时相距最远.
(2)由图看出1小时之内,两队相距最远距离是4千米;乙队追上甲队后,两队的距离也可计算,相比较得出甲、乙两队在出发后1小时相距最远.
解答:解:(1)乙队先达到终点,
对于乙队,x=1时,y=16,所以y=16x,
到达终点用时35÷16=
时=2时11分15秒,时间为11时11分15秒;
对于甲队,出发1小时后,设y与x关系为y=kx+b,
将x=1,y=20和x=2.5,y=35(5分)
别代入上式得:
解得
所以y=10x+10;
解方程组
得:x=
.
即出发1小时40分钟后(或者上午10点40分)乙队追上甲队;
(2)1小时之内,两队相距最远距离是4千米,
乙队追上甲队后,两队的距离是16x-(10x+10)=6x-10,当x为最大,
即x=
时,6x-10最大,
此时最大距离为6×
-10=3.125<4,
(也可以求出AD、CE的长度,比较其大小)
所以比赛过程中,甲、乙两队在出发后1小时(或者上午10时)相距最远.
对于乙队,x=1时,y=16,所以y=16x,
到达终点用时35÷16=
| 35 |
| 16 |
对于甲队,出发1小时后,设y与x关系为y=kx+b,
将x=1,y=20和x=2.5,y=35(5分)
别代入上式得:
|
解得
|
所以y=10x+10;
解方程组
|
| 5 |
| 3 |
即出发1小时40分钟后(或者上午10点40分)乙队追上甲队;
(2)1小时之内,两队相距最远距离是4千米,
乙队追上甲队后,两队的距离是16x-(10x+10)=6x-10,当x为最大,
即x=
| 35 |
| 16 |
此时最大距离为6×
| 35 |
| 16 |
(也可以求出AD、CE的长度,比较其大小)
所以比赛过程中,甲、乙两队在出发后1小时(或者上午10时)相距最远.
点评:本题考查一次函数的实际运用,利用待定系数法求一次函数关系式.当解决追程问题时,需注意的是两者路程相等.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 已知有理数a、b、c在数轴上对应的点如图,试化简:|b-a|-|a+c|-|b+c|.
已知有理数a、b、c在数轴上对应的点如图,试化简:|b-a|-|a+c|-|b+c|.