题目内容
18．
甲、乙两人同在如图所示的地下车库等电梯，已知两人都可以在1至4层的任意一层出电梯．（1）求甲从第3层楼出电梯的概率；
（2）用树状图或列表的方法求出甲、乙二人从同一层楼出电梯的概率．
分析 （1）根据总共有4种可能的情况，其中从第3层楼出电梯的情况有1种，即可得到甲从第3层楼出电梯的概率；
（2）列表得出所有等可能的情况数，找出甲乙在同一个楼层的情况数，即可求出所求的概率；
解答 解：（1）总共有4种可能的情况，其中从第3层楼出电梯的情况有1种，
∴P（甲从第3层楼出电梯）=$\frac{1}{4}$；
（2）列表如下：
甲 乙 | 1 | 2 | 3 | 4 |
| 1 | （1，1） | （2，1） | （3，1） | （4，1） |
| 2 | （1，2） | （2，2） | （3，2） | （4，2） |
| 3 | （1，3） | （2，3） | （3，3） | （4，3） |
| 4 | （1，4） | （2，4） | （3，4） | （4，4） |
∴P（甲、乙在同一层楼梯出电梯）=$\frac{4}{16}$=$\frac{1}{4}$．
点评 本题主要考查了列表法以及树状图法求概率，列表的目的在于不重不漏地列举出所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，求出概率．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
8．
如图，∠1与∠2是（ ）
如图，∠1与∠2是（ ）| A． | 对顶角 | B． | 同位角 | C． | 内错角 | D． | 同旁内角 |
9．
如图，小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°，则广告牌的高度BC约为（ ）（精确到0.1米）（sin35°=0.57，cos35°=0.82，tan35°=0.70；sin52°=0.79，cos52°=0.62，tan52°=1.28）
如图，小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°，则广告牌的高度BC约为（ ）（精确到0.1米）（sin35°=0.57，cos35°=0.82，tan35°=0.70；sin52°=0.79，cos52°=0.62，tan52°=1.28）| A． | 3.4米 | B． | 3.5米 | C． | 9.7米 | D． | 5.5米 |
6．下列公式不能用完全平方公式计算的是（ ）
| A． | （-2x-y）（2x+y） | B． | （-2x-y）（2x-y） | C． | （2x-y）（2x-y） | D． | （2x-y）（-2x+y） |
尺规作图：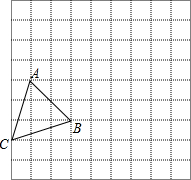
如图，将方格纸中的△ABC先向右平移6个单位长度，再向上平移4个单位，得到△A1B1C1．