题目内容
 如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是( )
如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是( )分析:根据垂直推出∠B+∠BAD=90°,∠BAD+∠CAE=90°,推出∠B=∠CAE,根据AD和AE不是对应边相等,即可判断A;根据AAS即可判断B;根据AAS即可判断C;根据AAS即可判断D.
解答:解:∵∠BAC=90°,BD⊥DE,CE⊥DE,
∴∠D=∠E=∠BAC=90°,
∴∠B+∠BAD=90°,∠BAD+∠CAE=90°,
∴∠B=∠CAE,
A、AD和AE不是对应边,即不能判断△ABD≌△CAE,故本选项正确;
B、在△ABD和△CAE中
,
∴△ABD≌△CAE(AAS),故本选项错误;
C、在△ABD和△CAE中
,
∴△ABD≌△CAE(AAS),故本选项错误;
D、在△ABD和△CAE中
,
∴△ABD≌△CAE(AAS),故本选项错误;
故选A.
∴∠D=∠E=∠BAC=90°,
∴∠B+∠BAD=90°,∠BAD+∠CAE=90°,
∴∠B=∠CAE,
A、AD和AE不是对应边,即不能判断△ABD≌△CAE,故本选项正确;
B、在△ABD和△CAE中
|
∴△ABD≌△CAE(AAS),故本选项错误;
C、在△ABD和△CAE中
|
∴△ABD≌△CAE(AAS),故本选项错误;
D、在△ABD和△CAE中
|
∴△ABD≌△CAE(AAS),故本选项错误;
故选A.
点评:本题考查了垂线和全等三角形的判定定理的应用,关键是能推出证明三角形全等的三个条件,主要培养学生运用定理进行推理的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,∠BAC=90°,AD⊥BC,△ABE,△ACF都是等边三角形,则S△ABE:S△ACF等于( )
如图,∠BAC=90°,AD⊥BC,△ABE,△ACF都是等边三角形,则S△ABE:S△ACF等于( )| A、AB:AC | B、AD2:DC2 | C、BD2:DC2 | D、AC2:AB2 |
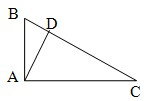 6、如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )
6、如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )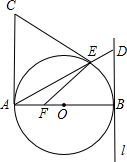 直线AE与l相交于点D.
直线AE与l相交于点D.
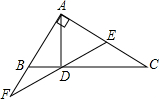
 已知:如图,∠BAC=90°,∠C=30°,AD⊥BC于D,DE⊥AB于E,BE=1,BC=
已知:如图,∠BAC=90°,∠C=30°,AD⊥BC于D,DE⊥AB于E,BE=1,BC=