题目内容
18.在平面上具有整数坐标的点称为整点,若有一线段的端点分别为(2,11),(11,14),则在此线段上(包括端点)的整点共有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 8个 |
分析 根据题意,设经过点(2,11)、(11,14)的直线方程y=ax+b(a≠0),利用待定系数法求得该直线方程,然后在此线段上(包括端点)寻找整点.
解答 解:设经过点(2,11)、(11,14)的直线方程y=ax+b(a≠0),则
$\left\{\begin{array}{l}{2a+b=11}\\{11a+b=14}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=\frac{31}{3}}\end{array}\right.$,
∴所求的线段所在的直线方程为y=$\frac{1}{3}$x+$\frac{31}{3}$;
①当y=12时,x=5,即整点(5,12)在该线段上;
②当y=13时,x=8,即整点(8,13)在该线段上;
又∵端点(2,11)、(11,14)也是整点,
∴在此线段上(包括端点)的整点共有4个,
故选:A.
点评 本题考查了坐标与图形性质.解得该题的关键是求得此线段所在的直线的方程,根据该直线方程取y的整数值.

练习册系列答案
相关题目
6.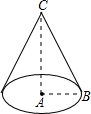 如图,在Rt△ABC中,∠BAC=90°,AB=2,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的表面积为( )
如图,在Rt△ABC中,∠BAC=90°,AB=2,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的表面积为( )
 如图,在Rt△ABC中,∠BAC=90°,AB=2,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的表面积为( )
如图,在Rt△ABC中,∠BAC=90°,AB=2,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的表面积为( )| A. | 10π | B. | 12π | C. | 14π | D. | 16π |
8.下列四组线段中,不能组成一个三角形的是( )
| A. | 6,6,3 | B. | 3,3,6 | C. | 3,3,5 | D. | 6,6,9 |
 如图,用12米长的铝合金做一个有横档的矩形窗子,横档长为x,矩形窗子的宽为y,则y关于x的函数解析式为y=-1.5x+6.
如图,用12米长的铝合金做一个有横档的矩形窗子,横档长为x,矩形窗子的宽为y,则y关于x的函数解析式为y=-1.5x+6.