题目内容
已知k=
=
=
,试判断直线y=kx+k一定经过 象限.
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
考点:一次函数图象与系数的关系,比例的性质
专题:
分析:由于a+b+c的符号不能确定,故进行分类讨论,当a+b+c≠0时,可利用等比性质求出k的值,当a+b+c=0时,可将a+b转化为-c,然后求出k,得到其解析式,进而判断出直线y=kx+k一定经过哪些象限.
解答:解:直线y=kx+k一定经过第二、三象限,理由如下:
当a+b+c≠0时,
∵
=
=
=k,
∴k=
=
,
此时,y=kx+k=
x+
,经过第一、二、三象限;
当a+b+c=0时,b+c=-a,此时,k=
=
=-1,
此时,y=kx+x=-x-1经过第二、三、四象限.
综上所述,y=kx+k一定经过第二、三象限,
故答案为:二、三.
当a+b+c≠0时,
∵
| a |
| b+c |
| b |
| a+c |
| c |
| a+b |
∴k=
| a+b+c |
| 2(a+b+c) |
| 1 |
| 2 |
此时,y=kx+k=
| 1 |
| 2 |
| 1 |
| 2 |
当a+b+c=0时,b+c=-a,此时,k=
| a |
| b+c |
| a |
| -a |
此时,y=kx+x=-x-1经过第二、三、四象限.
综上所述,y=kx+k一定经过第二、三象限,
故答案为:二、三.
点评:本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限.k<0时,直线必经过二、四象限.b>0时,直线与y轴正半轴相交.b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
相关题目
下列结论正确的是( )
A、单项式
| ||||
| B、32ab3的次数是6次 | ||||
| C、单项式-xyz的系数是-1,次数是4 | ||||
| D、多项式2x+xy-3是二次三项式 |
下列说法不正确的是( )
| A、5是25的算术平方根 | ||||
B、
| ||||
| C、16的平方根是-4 | ||||
| D、0的平方根与算术平方根都是0 |
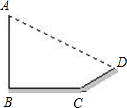 在同一时刻的物高与水平地面上的影长成正比例.小莉发现垂直地面的电线杆AB的影子落在地面和土坡上,影长分别为BC和CD,经测量得BC=20m,CD=8m,CD与地面成30°角,且此时测得垂直于地面的1m长标杆在地面上影长为2m,则电线杆AB的长度为
在同一时刻的物高与水平地面上的影长成正比例.小莉发现垂直地面的电线杆AB的影子落在地面和土坡上,影长分别为BC和CD,经测量得BC=20m,CD=8m,CD与地面成30°角,且此时测得垂直于地面的1m长标杆在地面上影长为2m,则电线杆AB的长度为 如图是用一张长方形纸条折成的,如果∠1=130°,那么∠2=
如图是用一张长方形纸条折成的,如果∠1=130°,那么∠2= 已知,如图:AB∥CD∥EF,∠B=∠C.求证:∠E=∠F.
已知,如图:AB∥CD∥EF,∠B=∠C.求证:∠E=∠F.