题目内容
2. 如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结0B,OC,若△ADE的周长为6cm,△OBC的周长为16cm.
如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结0B,OC,若△ADE的周长为6cm,△OBC的周长为16cm.(1)求线段BC的长;
(2)连结OA,求线段OA的长;
(3)若∠BAC=120°,求∠DAE的度数.
分析 (1)根据线段垂直平分线的性质得到DA=DB,EA=EC,根据三角形的周长公式计算即可;
(2)根据线段垂直平分线的性质和三角形的周长公式计算即可;
(3)根据线段垂直平分线的性质和等腰三角形的性质进行计算.
解答 解:(1)∵l1是AB边的垂直平分线,
∴DA=DB,
∵l2是AC边的垂直平分线,
∴EA=EC,
BC=BD+DE+EC=DA+DE+EA=6cm;
(2)∵l1是AB边的垂直平分线,
∴OA=OB,
∵l2是AC边的垂直平分线,
∴OA=OC,
∵OB+OC+BC=16cm,
∴OA=0B=OC=5cm;
(3)∵∠BAC=120°,
∴∠ABC+∠ACB=60°,
∵DA=DB,EA=EC,
∴∠BAD=∠ABC,∠EAC=∠ACB,
∴∠DAE=∠BAC-∠BAD-∠EAC=60°.
点评 本题考查的是线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.

练习册系列答案
相关题目
17.下列选项中,不是依据三角形全等知识解决问题的是( )
| A. | 利用尺规作图,作一个角等于已知角 | |
| B. | 工人师傅用角尺平分任意角 | |
| C. | 利用卡钳测量内槽的宽 | |
| D. | 用放大镜观察蚂蚁的触角 |
11.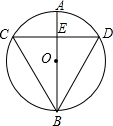 如图,AB是⊙O的直径,CD为弦,且CD⊥AB于E,则下列结论不正确的是( )
如图,AB是⊙O的直径,CD为弦,且CD⊥AB于E,则下列结论不正确的是( )
 如图,AB是⊙O的直径,CD为弦,且CD⊥AB于E,则下列结论不正确的是( )
如图,AB是⊙O的直径,CD为弦,且CD⊥AB于E,则下列结论不正确的是( )| A. | ∠BAC=∠BAD | B. | CE=DE | C. | $\widehat{BD}$=$\widehat{BC}$ | D. | OE=BE |
