题目内容
11.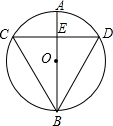 如图,AB是⊙O的直径,CD为弦,且CD⊥AB于E,则下列结论不正确的是( )
如图,AB是⊙O的直径,CD为弦,且CD⊥AB于E,则下列结论不正确的是( )| A. | ∠BAC=∠BAD | B. | CE=DE | C. | $\widehat{BD}$=$\widehat{BC}$ | D. | OE=BE |
分析 根据垂径定理对各选项进行逐一分析即可.
解答 解:A、∵AB是⊙O的直径,CD为弦,且CD⊥AB于E,
∴$\widehat{BC}$=$\widehat{BD}$,
∴∠BAC=∠BAD,故本选项正确;
B、∵AB是⊙O的直径,CD为弦,且CD⊥AB于E,
∴CE=DE,故本选项正确;
C、∵AB是⊙O的直径,CD为弦,且CD⊥AB于E,
∴$\widehat{BC}$=$\widehat{BD}$,故本选项正确;
D、∵点E不是OA的中点,∴OE与BE的长无法确定.
故选D.
点评 本题考查的是垂径定理,熟知平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
20.在△ABC中,∠A,∠B、∠C的对应边分别是a、b、c,若∠C=90°,则下列等式中成立的是( )
| A. | a2+b2=c2 | B. | b2+c2=a2 | C. | a2+c2=b2 | D. | b2-a2=c2 |
1.在等腰△ABC中,AB=AC,AB的垂直平分线DE与AC所在的直线相交于所成的锐角是40°,则∠B=( )
| A. | 40°或60° | B. | 65° | C. | 25°或65° | D. | 35°或125° |
 如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结0B,OC,若△ADE的周长为6cm,△OBC的周长为16cm.
如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结0B,OC,若△ADE的周长为6cm,△OBC的周长为16cm. 有一块长方形的土地,宽为120m,建筑商把它分成甲、乙、丙三部分,甲和乙均为正方形,现计划甲建住宅区,乙建商场,丙地开辟成面积为3200m2的公园.若设这块长方形的土地长为xm.那么根据题意列出的方程是x2-360x+32000=0.(将答案写成ax2+bx+c=0(a≠0)的形式)
有一块长方形的土地,宽为120m,建筑商把它分成甲、乙、丙三部分,甲和乙均为正方形,现计划甲建住宅区,乙建商场,丙地开辟成面积为3200m2的公园.若设这块长方形的土地长为xm.那么根据题意列出的方程是x2-360x+32000=0.(将答案写成ax2+bx+c=0(a≠0)的形式)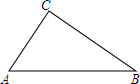 画图与说理:如图,在△ABC中.
画图与说理:如图,在△ABC中.