题目内容
 如图,△ABC中,点D为AB中点,CD=AD.
如图,△ABC中,点D为AB中点,CD=AD.(1)判断△ABC的形状,并说明理由;
(2)在图中画出△ABC的外接圆;
(3)已知AC=6,BC=8,点E是△ABC外接圆上任意一点,点M是弦AE的中点,当点E在△ABC外接圆上运动一周,求点M运动的路径长.
考点:作图—复杂作图,三角形的外接圆与外心
专题:
分析:(1)由三条线段相等CD=AD=BD,得到∠ACD=∠A,∠DCB=∠B,再由三角形内角和得出∠A+∠ACD+∠DCB+∠B=180°,所以∠ACB=∠ACD+∠DCB=90°△ABC为直角三角形.
(2)作AB和AC的中垂线交于点D,以D为圆心,AD为半径画圆,所得三角形就是△ABC的外接圆,因为CD=AD=BD,所以也可直接以D为圆心,AD为半径画圆,所得三角形就是△ABC的外接圆,
(3)连接DM.M是弦AE的中点,D为圆心,DM⊥AE,所以点M在以AD为直径的圆上运动.求出AD的长度,再求周长为点M的运动路径长为5π.
(2)作AB和AC的中垂线交于点D,以D为圆心,AD为半径画圆,所得三角形就是△ABC的外接圆,因为CD=AD=BD,所以也可直接以D为圆心,AD为半径画圆,所得三角形就是△ABC的外接圆,
(3)连接DM.M是弦AE的中点,D为圆心,DM⊥AE,所以点M在以AD为直径的圆上运动.求出AD的长度,再求周长为点M的运动路径长为5π.
解答:解:(1)△ABC为直角三角形.
理由如下:
∵CD=AD,
∴∠ACD=∠A.
又∵D为AB中点,
∴AD=BD,
∴CD=BD,
∴∠DCB=∠B.
∵∠A+∠ACD+∠DCB+∠B=180°,
∴∠ACB=∠ACD+∠DCB=90°,
∴△ABC为直角三角形.
(2)①如图,作AB和AC的中垂线交于点D,以D为圆心,AD为半径画圆,所得三角形就是△ABC的外接圆,
②也可直接以D为圆心,AD为半径画圆,所得三角形就是△ABC的外接圆,

(3)如图,连接DM.

∵M是弦AE的中点,D为圆心,
∴DM⊥AE,
∴点M在以AD为直径的圆上运动.
在Rt△ABC中,AC=6,BC=8,
∴AB=
=10,
∴AD=5.
∴点M的运动路径长为5π.
理由如下:
∵CD=AD,
∴∠ACD=∠A.
又∵D为AB中点,
∴AD=BD,
∴CD=BD,
∴∠DCB=∠B.
∵∠A+∠ACD+∠DCB+∠B=180°,
∴∠ACB=∠ACD+∠DCB=90°,
∴△ABC为直角三角形.
(2)①如图,作AB和AC的中垂线交于点D,以D为圆心,AD为半径画圆,所得三角形就是△ABC的外接圆,
②也可直接以D为圆心,AD为半径画圆,所得三角形就是△ABC的外接圆,

(3)如图,连接DM.

∵M是弦AE的中点,D为圆心,
∴DM⊥AE,
∴点M在以AD为直径的圆上运动.
在Rt△ABC中,AC=6,BC=8,
∴AB=
| AC2+BC2 |
∴AD=5.
∴点M的运动路径长为5π.
点评:本题主要考查了复杂作图,作外接圆及外心,解决本题的关键是找准外接圆的圆心,明确M的规迹是以AD为直径的圆.

练习册系列答案
相关题目
点A(1,y1)、B(2,y2)都在一次函数y=-2x+3的图象上,则y1、y2的大小关系是( )
| A、y1>y2 |
| B、y1=y2 |
| C、y1<y2 |
| D、不确定 |

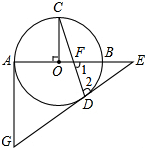 如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°. 如图,M为反比例函数y=
如图,M为反比例函数y=