Question

8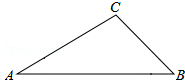．已知如图，在△ABC中，∠A=30°，∠C=105°，AC=$2\sqrt{3}$，求AB的长．

Answer 1

分析 根据三角形内角和定理求出∠B的度数，过C作CD⊥AB于D，根据等角对等边求出CD=BD，再根据在直角三角形中，30°角所对的直角边等于斜边的一半求出CD，根据勾股定理求出AD，最后根据AB=AD+BD，即可得出答案．

解答 解：在△ABC中，
∵∠A=30°，∠C=105°，
∴∠B=45°，
过C作CD⊥AB于D，
∴∠ADC=∠BDC=90°，
∵∠B=45°，
∴∠BCD=∠B=45°，
∴CD=BD，
∵∠A=30°，AC=2$\sqrt{3}$，
∴CD=$\sqrt{3}$，
∴BD=CD=$\sqrt{3}$，
由勾股定理得：AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=3，
∴AB=AD+BD=3+$\sqrt{3}$．

点评 此题考查了解直角三角形，用到的知识点是三角形内角和定理、勾股定理、在直角三角形中，30°角所对的直角边等于斜边的一半，关键是根据题意画出辅助线，构造直角三角形．