题目内容
10.根据下列材料,解答问题:等比数列求和:
概念:对于一列数a1,a2,a3,…an,…(n为正整数),若从第二个数开始,每一个数与前一个数的比为一定值,即$\frac{{a}_{k}}{{a}_{k-1}}$=q(常数),那么这一列数a1,a2,a3,…,an,…成等比数列,这一常数q叫做该数列的公比.
例:求等比数列$\frac{1}{3}$,$\frac{1}{{3}^{2}}$,$\frac{1}{{3}^{3}}$,…,$\frac{1}{{3}^{n}}$的和.
解:令S=$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{8}}$①,则3S=1+$\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{7}}$②
由②-①得:2S=1-$\frac{1}{{3}^{8}}$=$\frac{{3}^{8}-1}{{3}^{8}}$,即S=$\frac{{3}^{8}-1}{2×{3}^{8}}$.
(1)模仿例题,求等比数列$\frac{1}{4}$,$\frac{1}{{4}^{2}}$,$\frac{1}{{4}^{3}}$,…,$\frac{1}{{4}^{10}}$的和;
(2)填空:数列$\frac{1}{a}$,$\frac{1}{{a}^{2}}$,…$\frac{1}{{a}^{n}}$,(a≠1,n为正整数)的公比q=$\frac{1}{a}$,该数列各项的和为$\frac{{a}^{n}-1}{(a-1){a}^{n}}$.
分析 (1)仿造例题令S=$\frac{1}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+…+$\frac{1}{{4}^{10}}$,找出4S=1+$\frac{1}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+…+$\frac{1}{{4}^{9}}$,二者做差即可得出S的值;
(2)用后项除以前一项即可得出公比,仿造例题利用错位相减法即可找出数列$\frac{1}{a}$,$\frac{1}{{a}^{2}}$,…$\frac{1}{{a}^{n}}$,(a≠1,n为正整数)的各项之和.
解答 解:(1)令S=$\frac{1}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+…+$\frac{1}{{4}^{10}}$①,则4S=1+$\frac{1}{4}$+$\frac{1}{{4}^{2}}$+$\frac{1}{{4}^{3}}$+…+$\frac{1}{{4}^{9}}$②,
由②-①得:3S=1-$\frac{1}{{4}^{10}}$=$\frac{{4}^{10}-1}{{4}^{10}}$,
∴S=$\frac{{4}^{10}-1}{3×{4}^{10}}$.
(2)∵$\frac{\frac{1}{{a}^{2}}}{\frac{1}{a}}$=$\frac{1}{a}$,
∴q=$\frac{1}{a}$.
令S=$\frac{1}{a}$+$\frac{1}{{a}^{2}}$+…+$\frac{1}{{a}^{n}}$①,则$\frac{1}{a}$S=$\frac{1}{{a}^{2}}$+$\frac{1}{{a}^{3}}$+…+$\frac{1}{{a}^{n+1}}$②,
由①-②得:$\frac{a-1}{a}$S=$\frac{1}{a}$-$\frac{1}{{a}^{n+1}}$=$\frac{{a}^{n}-1}{{a}^{n+1}}$,
∴S=$\frac{{a}^{n}-1}{(a-1){a}^{n}}$.
故答案为:$\frac{1}{a}$;$\frac{{a}^{n}-1}{(a-1){a}^{n}}$.
点评 本题考查了规律型中的数字的变化类,利用错位相减法找出等比数列之和是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
 如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠ACD=$\frac{4}{5}$,BC=10,则AB的长为( )
如图,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos∠ACD=$\frac{4}{5}$,BC=10,则AB的长为( )| A. | 5 | B. | 6 | C. | 8 | D. | 5$\sqrt{3}$ |
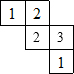 由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其正方形中的数字表示该位置上的小正方体的个数,画出该几何体的主视图.
由一些大小相同的小正方体搭成的几何体的俯视图如图所示,其正方形中的数字表示该位置上的小正方体的个数,画出该几何体的主视图. 如图,已知直线a∥b,直线c与a、b分别交于A、B,且∠1=120°,则∠2=120°.
如图,已知直线a∥b,直线c与a、b分别交于A、B,且∠1=120°,则∠2=120°.