题目内容
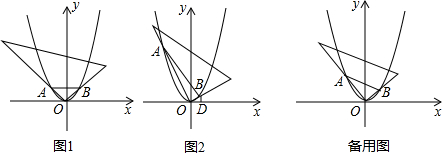
张亮是一个喜欢探究钻研的同学,他在和同学们一起研究某条抛物线y=ax2(a>0)的性质时,将一把直角三角形的直角顶点平面直角坐标系的原点O,两直角边与该抛物线交于A、B两点,请解答以下问题:
(1)若测得OA=OB=2
,(如图1),求a的值;
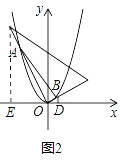
(2)对于同一条抛物线,张亮将三角板绕点O旋转到如图2位置时,过B作BD⊥x轴于点D,测得OD=1,写出此时点B的坐标,并求点A的横坐标;
(3)对该抛物线,张亮将三角板绕点O旋转任意角度时惊奇地发现,交点A、B的连线段总经过一个固定的点,试说明理由并求出该点的坐标.
(1)若测得OA=OB=2
| 2 |
(2)对于同一条抛物线,张亮将三角板绕点O旋转到如图2位置时,过B作BD⊥x轴于点D,测得OD=1,写出此时点B的坐标,并求点A的横坐标;
(3)对该抛物线,张亮将三角板绕点O旋转任意角度时惊奇地发现,交点A、B的连线段总经过一个固定的点,试说明理由并求出该点的坐标.

考点:二次函数综合题
专题:
分析:(1)先求出B点坐标,代入抛物线y=ax2(a<0)得a的值;
(2)过点A作AE⊥x轴于点E,可证△AEO∽△OFB,得出AE=2OE,可得方程点A的横坐标.
(3)设A(-m,
m2)(m>0),B(n,
n2)(n>0),易知△ACO∽△ODP,根据相似三角形的性质可知交点A、B的连线段总经过一个固定的点(0,2).
(2)过点A作AE⊥x轴于点E,可证△AEO∽△OFB,得出AE=2OE,可得方程点A的横坐标.
(3)设A(-m,
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)设线段AB与y轴的交点为C,由抛物线的对称性可得C为AB中点,
∵OA=OB=2
,∠AOB=90°,
∴AC=OC=BC=2,
∴B(2,2),
将B(2,2)代入抛物线y=ax2(a>0)得a=
;
(2)过点A作AE⊥x轴于点E,
∵点B的横坐标为1,
∴B(1,
),
∴BD=
.
∵∠AOB=90°,
∴∠AOE=∠OBF,
又∵∠AEO=∠OFB=90°,
∴△AEO∽△ODB,
∴
=
=2,
即AE=2OE,
设点A(-m,
m2)(m>0),则OE=m,AE=
m2,
∴
m2=2m,
∴m=4,即点A的横坐标为-4.
(3)设A(-m,
m2)(m>0),B(n,
n2)(n>0),
设直线AB的解析式为:y=kx+b,则
,
(1)×n+(2)×m得,(m+n)b=
(m2n+mn2)=
mn(m+n),
∴b=
mn,
又易知△AEO∽△ODB,
∴
=
,
∴
=
,
∴mn=4,
∴b=
×4=2,由此可知交点A、B的连线段总经过一个固定的点(0,2).
∵OA=OB=2
| 2 |
∴AC=OC=BC=2,
∴B(2,2),
将B(2,2)代入抛物线y=ax2(a>0)得a=
| 1 |
| 2 |
(2)过点A作AE⊥x轴于点E,
∵点B的横坐标为1,
∴B(1,
| 1 |
| 2 |
∴BD=
| 1 |
| 2 |

∵∠AOB=90°,
∴∠AOE=∠OBF,
又∵∠AEO=∠OFB=90°,
∴△AEO∽△ODB,
∴
| AE |
| OE |
| OD |
| BD |
即AE=2OE,
设点A(-m,
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴m=4,即点A的横坐标为-4.
(3)设A(-m,
| 1 |
| 2 |
| 1 |
| 2 |
设直线AB的解析式为:y=kx+b,则
|
(1)×n+(2)×m得,(m+n)b=
| 1 |
| 2 |
| 1 |
| 2 |
∴b=
| 1 |
| 2 |
又易知△AEO∽△ODB,
∴
| AE |
| OD |
| OE |
| BD |
∴
| 0.5m2 |
| n |
| m |
| 0.5n2 |
∴mn=4,
∴b=
| 1 |
| 2 |
点评:本题是对二次函数的综合考查,有等腰直角三角形的性质,坐标与图形的变化,相似三角形的判定与性质,旋转变换的性质,待定系数法求函数解析式,综合性较强,难度较大.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图,已知∠AOB=40°,自O点引射线OC,若∠AOC:∠COB=2:3,OC与∠AOB的平分线所成的角的度数为
如图,已知∠AOB=40°,自O点引射线OC,若∠AOC:∠COB=2:3,OC与∠AOB的平分线所成的角的度数为 如图,将含60°角的直角三角极ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′.若∠BAC=60°,AC=1,则图中阴影部分的面积是
如图,将含60°角的直角三角极ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′.若∠BAC=60°,AC=1,则图中阴影部分的面积是