题目内容
14.在平面直角坐标系中有线段AB和点A′,已知A点的坐标为(-2,1),B点的坐标为(-3,-2),A′点的坐标为(1,2),分别按下列要求完成各题.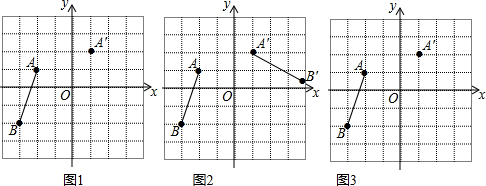
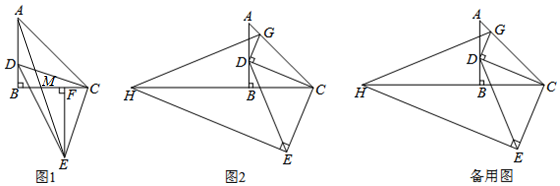
(1)如图1,平移线段AB,使点A移到点A′的位置,请在图中作出平移后的线段A′B′,并直接写出B′点的坐标为(0,-1);
(2)如图2,线段AB与A′B′关于某条直线l对称,请用尺规作图的方法在图中画出对称轴l(保留作图痕迹),并直接写出对称轴l的解析式为y=-3x;
(3)如图3,线段AB绕图中某点P顺时针方向旋转90°,点A恰好旋转到点A′的位置,请在图中画出点P的位置,并画出点B的对应点B′,直接写出:P点的坐标为(0,0),在旋转过程中线段AB扫过的面积为2π.
分析 (1)根据图形平移的性质画出图形,写出B′点的坐标即可;
(2)连接AA′,作线段AA′的垂直平分线,利用待定系数法求出对称轴l的解析式即可;
(3)连接AA′,作线段AA′的垂直平分线,连接OA,OB′可知旋转中心为点O,根据图形旋转的性质找出B′点,根据扇形的面积公式即可得出旋转过程中线段AB扫过的面积.
解答 解:(1)如图1所示,B′(0,-1).
故答案为:(0,-1);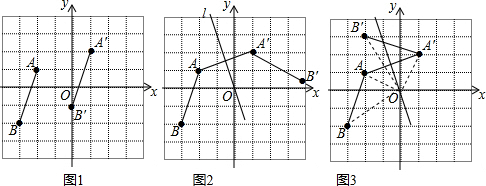
(2)如图2所示,
连接AA′,作线段AA′的垂直平分线,则此直线即为直线l.
由图可知,直线l过点(0,0),(-1,3),
∴设直线l的解析式为y=kx(k≠0),
∵直线过点(-1,3),
∴3=-k,即k=-3,
∴直线l的解析式为:y=-3x.
故答案为:y=-3x;
(3)如图3所示,
∵OA=OA′,且∠AOA′=90°,
∴点O即为P点.
∵OA=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,OB=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
∴在旋转过程中线段AB扫过的面积=$\frac{90×π×[(\sqrt{13})^{2}-(\sqrt{5})^{2}]}{360}$=2π.
故答案为:(0,0),2π.
点评 本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
5.某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8:00~12:00,下午14:00~18:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于45件.
生产产品件数与所用时间之间的关系见下表:
信息三:按件计酬,每生产一件甲产品可得6元,每生产一件乙产品可得10元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
信息一:工作时间:每天上午8:00~12:00,下午14:00~18:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于45件.
生产产品件数与所用时间之间的关系见下表:
| 生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(分) |
| 10 | 10 | 500 |
| 15 | 20 | 900 |
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
9.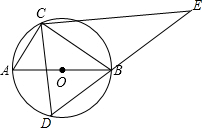 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )
 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )| A. | 2$\sqrt{5}$ | B. | 5$\sqrt{5}$ | C. | $\frac{16\sqrt{5}}{5}$ | D. | 4$\sqrt{5}$ |
19.近期由于雾霾严重,不少市民选择佩戴口罩出行,某药店购进甲种可预防PM2.5的N95型口罩和乙种普通口罩共400个,这两种口罩的进价和售价如表所示:
该药店计划购进乙种口罩x个,两种口罩全部销售完后可获毛利润y元.
注:毛利润=(售价-进价)×销售量
(1)求出毛利润y与x的函数关系式;
(2)已知甲种口罩的数量不多于乙种口罩数量的3倍,该药店怎样进货,使全部销售获得的毛利润最大?并求出最大毛利润.
| 甲 | 乙 | |
| 进价(元/个) | 18 | 6 |
| 售价(元/个) | 22 | 9 |
注:毛利润=(售价-进价)×销售量
(1)求出毛利润y与x的函数关系式;
(2)已知甲种口罩的数量不多于乙种口罩数量的3倍,该药店怎样进货,使全部销售获得的毛利润最大?并求出最大毛利润.
6. 在平面直角坐标系中,设坐标的单位长度为1cm,点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题.
在平面直角坐标系中,设坐标的单位长度为1cm,点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题.
(1)填表:
(2)当点P从点O出发15秒,可得到的整点的个数是16个;
(3)当点P从O点出发17秒时,可得到整点(9,8).
 在平面直角坐标系中,设坐标的单位长度为1cm,点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题.
在平面直角坐标系中,设坐标的单位长度为1cm,点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题.(1)填表:
| P从O出发的时间 | 可以得到的整点的坐标 | 可以得到的整点的个数 |
| 1秒 | (0,1)、(1,0) | 2个 |
| 2秒 | (2,0)、(0,2)、(1,1) | 3 |
| 3秒 | (3,0)、(0,3)、(1,2)、(2,1) | 4 |
(3)当点P从O点出发17秒时,可得到整点(9,8).
 如图,在△ABC中,M、E把AC边三等分,MN∥EF∥BC,MN、EF把△ABC分成三部分,则自上而下三部分的面积比为1:3:5.
如图,在△ABC中,M、E把AC边三等分,MN∥EF∥BC,MN、EF把△ABC分成三部分,则自上而下三部分的面积比为1:3:5.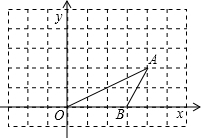 如图,点O、B的坐标分别为(0,0)、(3,0),将△OAB绕点O按逆时针方向旋转90°△OA′B′.
如图,点O、B的坐标分别为(0,0)、(3,0),将△OAB绕点O按逆时针方向旋转90°△OA′B′.