题目内容
 B,C是河岸边两点,A为对岸岸上一点,测得∠ABC=45°,∠ACB=45°,BC=50m,则河宽AD为
B,C是河岸边两点,A为对岸岸上一点,测得∠ABC=45°,∠ACB=45°,BC=50m,则河宽AD为
- A.25
 m
m - B.25m
- C.

 m
m - D.25
 m
m
B
分析:根据题意,构建直角三角形,利用等腰直角三角形的性质即可解答.
解答: 解:根据题意画出图形,过A作AD⊥BC于D,因为∠ABC=45°,∠ACB=45°,BC=50m,
解:根据题意画出图形,过A作AD⊥BC于D,因为∠ABC=45°,∠ACB=45°,BC=50m,
所以AB=AC,BD=CD= BC=
BC= ×50m=25m,∠ADB=90°,
×50m=25m,∠ADB=90°,
在Rt△ABD中,∠B=45°,∠ADB=90°,∴∠BAD=∠B=45°,BD=AD=25m.
故选B.
点评:本题考查的是勾股定理及等腰三角形的性质在实际生活中的运用,锻炼了学生对所学知识的运用能力.
分析:根据题意,构建直角三角形,利用等腰直角三角形的性质即可解答.
解答:
 解:根据题意画出图形,过A作AD⊥BC于D,因为∠ABC=45°,∠ACB=45°,BC=50m,
解:根据题意画出图形,过A作AD⊥BC于D,因为∠ABC=45°,∠ACB=45°,BC=50m,所以AB=AC,BD=CD=
 BC=
BC= ×50m=25m,∠ADB=90°,
×50m=25m,∠ADB=90°,在Rt△ABD中,∠B=45°,∠ADB=90°,∴∠BAD=∠B=45°,BD=AD=25m.
故选B.
点评:本题考查的是勾股定理及等腰三角形的性质在实际生活中的运用,锻炼了学生对所学知识的运用能力.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 B,C是河岸边两点,A为对岸岸上一点,测得∠ABC=45°,∠ACB=45°,BC=50m,则河宽AD为( )
B,C是河岸边两点,A为对岸岸上一点,测得∠ABC=45°,∠ACB=45°,BC=50m,则河宽AD为( )A、25
| ||||
| B、25m | ||||
C、
| ||||
D、25
|
 如图,B、C是河岸边两点,A是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60 m,则点A到对岸BC的距离是
如图,B、C是河岸边两点,A是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60 m,则点A到对岸BC的距离是 如图,B,C是河岸边两点,A是对岸边上的一点,测得∠ABC=30°,∠ACB=60°,BC=50米,则A到岸边BC的距离是
如图,B,C是河岸边两点,A是对岸边上的一点,测得∠ABC=30°,∠ACB=60°,BC=50米,则A到岸边BC的距离是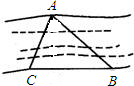 如图,B,C是河岸边两点,A是对岸边上一点,测得∠ABC=45°,∠ACB=60°,BC=60米,甲想从A点出发在最短的时间内到达BC边,若他的速度为5米/分,则他所用的最短时间为
如图,B,C是河岸边两点,A是对岸边上一点,测得∠ABC=45°,∠ACB=60°,BC=60米,甲想从A点出发在最短的时间内到达BC边,若他的速度为5米/分,则他所用的最短时间为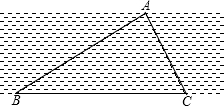 如图,B、C是河岸边两点,A是对岸边上的一点,测得∠ABC=30°,∠ACB=45°,BC的长是30米,求河的宽度.(结果保留根号)
如图,B、C是河岸边两点,A是对岸边上的一点,测得∠ABC=30°,∠ACB=45°,BC的长是30米,求河的宽度.(结果保留根号)