题目内容
如图，AD⊥BC，∠1=40°，∠2=30°，则∠B=考点：三角形内角和定理
专题：
分析：先根据AD⊥BC得出∠ADB=∠AC=90°，再根据两角互补的性质即可得出结论．
解答：解：∵AD⊥BC，
∴∠ADB=∠AC=90°，
∵∠1=40°，
∴∠B=90°-40°=50°；
∵∠2=30°，
∴∠C=90°-30°=60°．
故答案为：50°，60°．
∴∠ADB=∠AC=90°，
∵∠1=40°，
∴∠B=90°-40°=50°；
∵∠2=30°，
∴∠C=90°-30°=60°．
故答案为：50°，60°．
点评：本题考查的是三角形内角和定理，熟知“三角形的内角和等于180°”是解答此题的关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
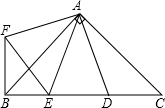如图，在Rt△ABC中，AB=AC，D，E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连结EF．则∠EAF=
如图，?ABCD的面积为20，E，F，G为对角线AC的四等分点，连接BE并延长交AD于H，连接HF并延长交BC于点M，则△BHM的面积为（ ）在下列条件中能判定△ABC为直角三角形的是（ ）
| A、∠A+∠B=2∠C | ||||
| B、∠A=∠B=30° | ||||
| C、∠A=2∠B=3∠C | ||||
D、∠A=
|