Question

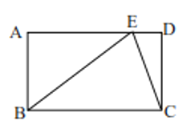
【题目】如图，Rt△ABC中，∠ABC＝90°，以AB为直径的⊙O交AC于点D，E是BC的中点，连接DE、OE．

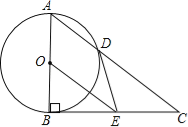
(1)判断DE与⊙O的位置关系并说明理由；

(2)若⊙O半径r=3，DE＝4，求AD的长．

Answer 1

【答案】(1) DE与⊙O相切； (2)3.6

【解析】

（1）连接OD，BD；∵AB为直径，∴，，则△BDC为Rt△；又∵E是BC的中点 ∴DE是Rt△BDC斜边上的中线，所以DE=CE，所以；∵OA=OD，∴；如图，Rt△ABC中，∠ABC＝90°则，即，所以，∴DE与⊙O相切；

（2）由（1）知DE=CE=4；，∴；∵E是BC的中点，∴BC=2CE=8；若⊙O半径r=3，则AB=2r=6；在t△ABC中由勾股定理得AC=10；根据三角形的面积相等得；解得BD=4.8，∴.