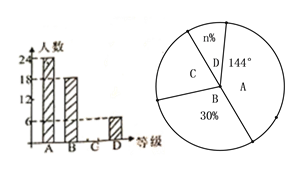题目内容
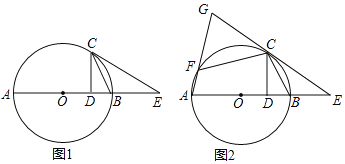
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上的一个动点,过
是抛物线上的一个动点,过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)直接写出![]() ,
,![]() ,
,![]() 三点的坐标;
三点的坐标;
(2)若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求此时点
为顶点的四边形是平行四边形,求此时点![]() 的坐标;
的坐标;
(3)当点![]() 位于直线
位于直线![]() 下方的抛物线上时,过点
下方的抛物线上时,过点![]() 作
作![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求
的函数关系式,并求![]() 的最大值.
的最大值.

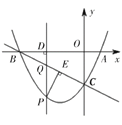
【答案】(1)![]() 、
、![]() 、
、![]() ;(2)
;(2)![]() 点坐标为
点坐标为![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)根据抛物线与坐标轴的交点可得A,B,C三点的坐标;
(2)求出直线解析式,根据平行四边形的性质可求解;
(3)设点P的坐标为![]() ,则可用含m的代数式表示点Q的坐标;可求得BQ的长,证明
,则可用含m的代数式表示点Q的坐标;可求得BQ的长,证明![]() ,得出
,得出![]() ,可用含m的代数式表示QE和PE的长度,根据面积计算公式和抛物线顶点式方程可求解.
,可用含m的代数式表示QE和PE的长度,根据面积计算公式和抛物线顶点式方程可求解.
解:(1)当![]() 时,
时,![]() 即
即![]()
当![]() 时,有:
时,有:![]()
解得![]() 即
即![]() 、
、![]()
故:![]() 、
、![]() 、
、![]()
(2)设直线![]() 解析式为
解析式为![]() ,
,
∵![]() ,
,![]() ,
,
∴代入可得![]() ,解得
,解得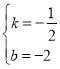 ,∴直线
,∴直线![]() 解析式为
解析式为![]() ,
,
设![]() 坐标为
坐标为![]() ,则
,则![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,
由题意可知,![]() ,当
,当![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形时,则有
为顶点的四边形为平行四边形时,则有
![]() ,
,
即![]() ,或
,或![]()
解得![]() ,
,![]() ,
,![]() ,
,
综上可知![]() 点坐标为
点坐标为![]() 或
或 ![]() 或
或![]() ;
;
(3)![]() 点坐标为
点坐标为![]() ,则
,则![]() 点坐标为
点坐标为![]() ,
,
![]() ,
,![]() 在
在![]() 中,
中,![]() ;
;
又![]()
∵![]() ,
,![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
![]()
∴![]()
令![]() ,
,
∵![]() 在直线
在直线![]() 下方
下方
∴当![]() 时,
时,![]() 有最小值
有最小值![]() ,
,![]() 点坐标为
点坐标为![]() ,此时
,此时![]() 取最大值为
取最大值为![]()

 黎明文化寒假作业系列答案
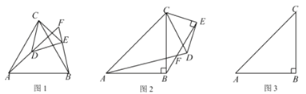
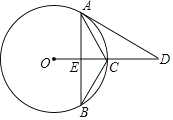
黎明文化寒假作业系列答案【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
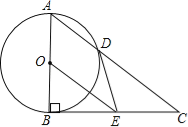
(1)判断DE与⊙O的位置关系并说明理由;
(2)若⊙O半径r=3,DE=4,求AD的长.
【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下统计图:

(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为___________度
(2)请补充完整下面的成绩统计分析表:
平均数 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 |
|
乙组 | 1.36 |
|
(3)你认为那组成绩较好?从以上信息中写出两条支持你的选择
(4)从甲、乙两组得9分的学生中抽取两人参加市级比赛,求这两人来自不同组的概率