题目内容
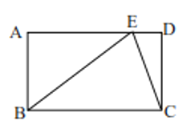
【题目】已知：如图，点E是矩形ABCD的边AD上一点，BE＝AD，AE＝8，现有甲乙二人同时从E点出发，分别沿EC、ED方向前进，甲的速度是乙的
倍，甲到达点目的地C点的同时乙恰巧到达终点D处．
（1）求tan∠ECD的值
（2）求线段AB及BC的长度．
【答案】（1）
；（2）AB＝
，BC＝
【解析】
（1）设ED＝x ，则EC＝
x，在Rt△EDC中根据勾股定理用x表示出CD的长，由锐角三角函数的定义即可得出结论；
（2）根据tan∠ECD＝，设ED＝x，CD＝2x，表达出BE，再在Rt△ABE中，利用勾股定理得到AE2＋AB2＝BE2，列出方程解出x＝
，从而求出AB，BC的值即可
解：（1）∵四边形ABCD是矩形，
∴∠D是直角．
根据条件：甲的速度是乙的倍，设ED＝x ，则EC＝x，
∴在Rt△EDC中CD＝
= 2x，
∴tan∠ECD＝
＝．
（2）∵四边形ABCD是矩形，
∴设ED＝x，AB＝CD＝2x．
∵BE＝AD，AE＝8，
∴BE＝AD＝8＋x．
∵在Rt△ABE中，AE2＋AB2＝BE2
∴82＋（2x）2＝（8＋x）2，
∴x＝，或x＝0（不合题意，舍）
∴AB＝2x＝，BC＝AD＝8＋x＝．
练习册系列答案
相关题目
