题目内容
 如图,EF、EG分别是∠AEB、∠BEC的平分线,则∠GEF的度数是
如图,EF、EG分别是∠AEB、∠BEC的平分线,则∠GEF的度数是考点:角平分线的定义
专题:
分析:根据角平分线的定义得出∠BEF=
∠BEA,∠GEB=
∠BEC,于是∠GEF=∠BEF+∠GEB=
∠AEC=90°.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵EF、EG分别是∠AEB、∠BEC的平分线,
∴∠BEF=
∠BEA,∠GEB=
∠BEC,
∴∠GEF=∠BEF+∠GEB=
∠BEA+
∠BEC=
(∠BEA+∠BEC)=
∠AEC=90°.
故答案为90°.
∴∠BEF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠GEF=∠BEF+∠GEB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为90°.
点评:本题考查了角平分线的定义,邻补角定义,解答本题的关键是根据角平分线的定义得出∠BEF=
∠BEA,∠GEB=
∠BEC,难度一般.
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目
平面上有10个点,没有三点在一条直线上,以一个点A为顶点的三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
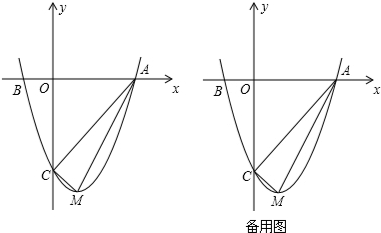
 如图,在等腰△ABC中,∠ABC=90°,点D为BC的中点,点E在AC边上,以DE为腰作等腰Rt△DEF,连接CF,BF.若CE=1,△CDF的面积为7.5,则BF的长为
如图,在等腰△ABC中,∠ABC=90°,点D为BC的中点,点E在AC边上,以DE为腰作等腰Rt△DEF,连接CF,BF.若CE=1,△CDF的面积为7.5,则BF的长为