题目内容
8.若x<-4,化简|-3|+|x+4|-|x-4|-|-x+2|.分析 根据x的取值范围,利用绝对值的意义先化简,再进一步合并得出答案即可.
解答 解:∵x<-4,
∴|-3|+|x+4|-|x-4|-|-x+2|
=3-x+4-(x-4)-(-x+2)
=3-x-x+4+x-2
=5-x.
点评 此题考查整式的加减,利用绝对值的意义化简,掌握合并同类项的方法是解决问题的关键.

练习册系列答案
相关题目
16. 如图,C是AB的黄金分割点,那么$\frac{AC}{AB}$与$\frac{AC}{BC}$的值分别是( )
如图,C是AB的黄金分割点,那么$\frac{AC}{AB}$与$\frac{AC}{BC}$的值分别是( )
 如图,C是AB的黄金分割点,那么$\frac{AC}{AB}$与$\frac{AC}{BC}$的值分别是( )
如图,C是AB的黄金分割点,那么$\frac{AC}{AB}$与$\frac{AC}{BC}$的值分别是( )| A. | $\frac{\sqrt{5}+1}{2}$,$\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}-1}{2}$,$\frac{\sqrt{5}+1}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$,$\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{5}+1}{2}$,$\frac{\sqrt{5}+1}{2}$ |
18.已知am=5,an=6,则am+n的值为( )
| A. | 11 | B. | 30 | C. | $\frac{5}{6}$ | D. | $\frac{6}{5}$ |
 如图,△ABC中,AB与BC的夹角是∠B,∠A的对边是CB,∠A、∠C的公共边是AC.
如图,△ABC中,AB与BC的夹角是∠B,∠A的对边是CB,∠A、∠C的公共边是AC.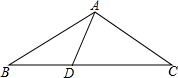 如图,在△ABC中,D是BC边上一点,AD=BD,AB=AC=CD,求∠ADC的度数.
如图,在△ABC中,D是BC边上一点,AD=BD,AB=AC=CD,求∠ADC的度数.