题目内容
18.等腰梯形的对角线长为17cm,上、下底分别为10cm,20cm,则梯形面积为120cm2.分析 过D作DE∥AC交BC延长线于E,DF⊥BC于F,推出四边形ACED是平行四边形,根据平行四边形的性质得出AD=CE=10cm,AC=DE=BD=17cm,根据等腰三角形的性质求出BF=EF=$\frac{1}{2}$BE=15cm,在Rt△BDF中,由勾股定理求出DF,根据梯形的面积公式求出即可.
解答 解:如图,过D作DE∥AC交BC延长线于E,DF⊥BC于F,
∵AD∥BC,
∴四边形ACED是平行四边形,
∴AD=CE=10cm,AC=DE=BD=17cm,
∵DF⊥BC,BD=DE,
∴BF=EF=$\frac{1}{2}$BE=$\frac{1}{2}×$(10cm+20cm)=15cm,
在Rt△BDF中,由勾股定理得:DF=$\sqrt{1{7}^{2}-1{5}^{2}}$=8(cm),
∴梯形ABCD的面积S=$\frac{1}{2}$(AD+BC)DF=$\frac{1}{2}$×(10cm+20cm)×8cm=120cm2
故答案为:120cm2.
点评 本题考查了等腰梯形的性质,等腰三角形的性质,勾股定理,平行四边形的性质和判定的应用,解此题的关键是能求出梯形的高.

练习册系列答案
相关题目
3.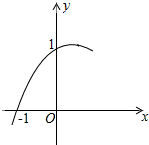 如图是二次函数y=ax2+bx+c是图象的一部分,记M=a+b,则M的取值范围是( )
如图是二次函数y=ax2+bx+c是图象的一部分,记M=a+b,则M的取值范围是( )
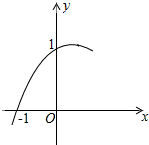 如图是二次函数y=ax2+bx+c是图象的一部分,记M=a+b,则M的取值范围是( )
如图是二次函数y=ax2+bx+c是图象的一部分,记M=a+b,则M的取值范围是( )| A. | -1<M<0 | B. | -1<M<1 | C. | 0<M<1 | D. | 不能确定 |
7.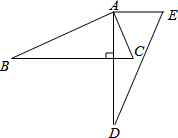 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,且AD⊥BC.若∠CAE=65°,∠E=60°,则∠BAC的大小为( )
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,且AD⊥BC.若∠CAE=65°,∠E=60°,则∠BAC的大小为( )
 如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,且AD⊥BC.若∠CAE=65°,∠E=60°,则∠BAC的大小为( )
如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE,且AD⊥BC.若∠CAE=65°,∠E=60°,则∠BAC的大小为( )| A. | 60° | B. | 75° | C. | 85° | D. | 95° |
8.下列四个命题中是假命题的是( )
| A. | 若a>b,则a-c>b-c | B. | 同位角一定相等 | ||
| C. | 若∠1+∠2=180°,则∠1与∠2互为补角 | D. | 平行于同一条直线的两条直线平行 |
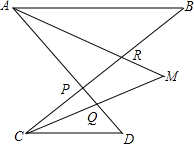 如图,∠B=36°,∠D=50°,AM,CM分别平分∠BAD和∠BCD,AM交BC于点R,CM交AD于点Q,BC与AD交于点P,求∠M的度数.
如图,∠B=36°,∠D=50°,AM,CM分别平分∠BAD和∠BCD,AM交BC于点R,CM交AD于点Q,BC与AD交于点P,求∠M的度数.