题目内容
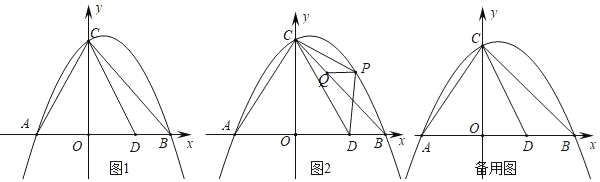
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() )和B(4,6),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,6),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)当C为抛物线顶点的时候,求![]() 的面积.
的面积.
(3)是否存在质疑的点P,使![]() 的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.
的面积有最大值,若存在,求出这个最大值,若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() (3)存在,
(3)存在,![]() (m为点P的横坐标)当m=
(m为点P的横坐标)当m=![]() 时,
时,![]()
![]()
【解析】
(1)把A、B坐标代入二次函数解析式,求出a、b,即可求得解析式;
(2)根据第(1)问求出的函数解析式可得出C点的坐标,根据C、P两点横坐标一样可得出P点的坐标,将△BCE的面积分成△PCE与△PCB,以PC为底,即可求出△BCE的面积.
(3)设动点P的坐标为(m,m+2),点C的坐标为(m,![]() ),表示出PC的长度,根据
),表示出PC的长度,根据![]() ,构造二次函数,然后求出二次函数的最大值,并求出此时m的值即可.
,构造二次函数,然后求出二次函数的最大值,并求出此时m的值即可.
解:(1)∵A(![]() )和B(4,6)在抛物线y=ax2+bx+6上,
)和B(4,6)在抛物线y=ax2+bx+6上,
∴
解得:![]() ,
,
∴抛物线的解析式![]() ;
;
(2)∵二次函数解析式为![]() ,
,
∴顶点C坐标为![]() ,
,
∵PC⊥x,点P在直线y=x+2上,
∴点P的坐标为![]() ,
,
∴PC=6;
∵点E为直线y=x+2与x轴的交点,
∴点E的坐标为![]()
∵ ![]() =
=![]()
∴![]() .
.
(3)存在.
设动点P的坐标是![]() ,点C的坐标为
,点C的坐标为![]() ,
,
∵![]()
![]()
∴![]()
∵![]() ,
,
∴函数开口向下,有最大值
∴当![]() 时,△ABC的面积有最大值为
时,△ABC的面积有最大值为![]() .
.

练习册系列答案
相关题目