题目内容
【题目】如图，已知
和
，点
在
边上，
，边
与
相交于点
．
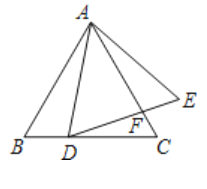
（1）求证：
；
（2）如果
，求证：
．
【答案】（1）见解析；（2）见解析
【解析】
（1）根据等边对等角得到
，通过证明△ABC∽△FDA得对应边成比例，化比例式为等积式即可；
（2）通过证明△AEF∽△CDF和△ABD∽△EDA,根据相似三角形的性质列两个比例式，用等量代换即可得.
（1）证明：∵AD=DC,
∴∠DAC=∠C,
∵∠ADE=∠B,
∴△ABC∽△FDA,
∴
,
∴
.
（2）证明：∵AE∥BC,
∴∠E=∠EDC, ∠EAC=∠C,
∴△AEF∽△CDF,
∴
,
∴
,
∵∠ADC=∠ADE+∠EDC=∠B+∠BAD, ∠ADE=∠B,
∴∠BAD=∠EDC,
∴∠BAD=∠E,
∴△ABD∽△EDA,
∴
,
∴
,
∴
.
练习册系列答案
相关题目
【题目】已知二次函数y＝ax2+bx+c中，函数y与自变量x的部分对应值如表：
x | … | ﹣1 | 0 | 1 | 2 | 4 | … |
y | … | 10 | 1 | ﹣2 | 1 | 25 | … |
（1）求这个二次函数的解析式；
（2）写出这个二次函数图象的开口方向、对称轴和顶点坐标．
