题目内容
12.已知有理数x,y,z满足条件:|x-z-2|+|3x-6y-7|+(3y+3z-4)2=0,则xyz=1.分析 已知等式为三个非负数的和为0的形式,只有这几个非负数都为0,可组成方程组,求x、y、z的值,即可求得xyz的值.
解答 解:根据非负数的性质,得$\left\{\begin{array}{l}{x-z-2=0①}\\{3x-6y-7=0②}\\{3y+3z-4=0③}\end{array}\right.$
①×3-②,得6y-3z+1=0④
④+③,得9y=3,
解得y=$\frac{1}{3}$,
把y=$\frac{1}{3}$代入④得z=1,
把z=1代入①得x=3.
∴xyz=3×$\frac{1}{3}$×1=1.
故答案为1.
点评 考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0,三元一次方程组的解法,代数式求值,综合题,难度较大.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
2.已知x=2是关于x的一元一次方程mx+2=0的解,则m的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
8. 如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
 如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )
如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为( )| A. | 34° | B. | 56° | C. | 66° | D. | 54° |
 画出如图所示物体的主视图、左视图、俯视图.
画出如图所示物体的主视图、左视图、俯视图. ∥
∥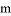 ,∠1=120°,∠A=55°,则∠ACB的大小是______.
,∠1=120°,∠A=55°,则∠ACB的大小是______.