题目内容
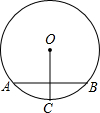 如图,⊙O的一条弦AB垂直平分半径OC,且AB=2
如图,⊙O的一条弦AB垂直平分半径OC,且AB=2| 3 |
| A、6 | ||
B、6
| ||
| C、12 | ||
D、12
|
考点:正多边形和圆
专题:
分析:如图,作辅助线;首先求出该正多边形的中心角;运用勾股定理求出半径R;求出△OCD的面积,即可解决问题.
解答: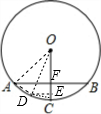 解:如图,连接OA;取
解:如图,连接OA;取
的中点D,
连接AD、CD、OD;
过点D作DE⊥OC于点E;
∵OF=
OA,且∠OFA=90°,
∴∠OAF=30°,∠AOC=60°,∠AOD=∠COD=30°;
∵圆的内接正十二边形的中心角=
=30°,
∴AD、DC为该圆的内接正十二边形的两边;
∵OC⊥AB,且AB=2
,
∴AF=
;在△AOF中,由勾股定理得:
R2=(
R)2+(
)2,解得:R=2;
在△ODE中,∵∠EOD=30°,
∴DE=
OD=1,S△OCD=
OC•DE=1,
∴这个圆的内接正十二边形的面积为12.
故选C.
 解:如图,连接OA;取
解:如图,连接OA;取 |
| AC |
连接AD、CD、OD;
过点D作DE⊥OC于点E;
∵OF=
| 1 |
| 2 |
∴∠OAF=30°,∠AOC=60°,∠AOD=∠COD=30°;
∵圆的内接正十二边形的中心角=
| 360° |
| 12 |
∴AD、DC为该圆的内接正十二边形的两边;
∵OC⊥AB,且AB=2
| 3 |
∴AF=
| 3 |
R2=(
| 1 |
| 2 |
| 3 |
在△ODE中,∵∠EOD=30°,
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴这个圆的内接正十二边形的面积为12.
故选C.
点评:该题主要考查了正多边形和圆的关系及其应用问题;解题的关键是作辅助线,求出该正多边形的半径、中心角.

练习册系列答案
相关题目
下列各组数中互为相反数的是( )
| A、+(+5)与-(-5) | ||
| B、+(-5)与-(+5) | ||
C、+(+5)与-(-
| ||
| D、+(-5)与-(-5) |
 如图,点B,F,C,E在同一条直线上,∠A=∠D,FG=GC,若AB=6cm,BC=8cm,CE=DE=3cm,求线段FC的长.
如图,点B,F,C,E在同一条直线上,∠A=∠D,FG=GC,若AB=6cm,BC=8cm,CE=DE=3cm,求线段FC的长. 如图,抛物线y=-x2+2x+m与x轴相交于点A(3,0)和B,与y轴相交于点C.
如图,抛物线y=-x2+2x+m与x轴相交于点A(3,0)和B,与y轴相交于点C. 点C在线段AB上,线段AC=6,BC=4,点M,N分别是AC和BC的中点
点C在线段AB上,线段AC=6,BC=4,点M,N分别是AC和BC的中点 如图,把△ABC绕C顺时针旋转35°,得到△A′B′C,若∠BCA′=100°,则∠B′CA=
如图,把△ABC绕C顺时针旋转35°,得到△A′B′C,若∠BCA′=100°,则∠B′CA=