题目内容
4.一透明的敞口正方体容器ABCD-A′B′C′D′装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE=α,如图所示).
探究:如图1,液面刚好过棱CD,并与棱BB′交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图②.
解决问题:
(1)CQ与BE的位置关系是CQ∥BE,BQ的长是3dm,α=37°(注:sin49°=cos41°=$\frac{3}{4}$,tan37°=$\frac{3}{4}$)
(2)求液体的体积;(参考算法:直棱柱体积V液=底面积SBCQ×高AB)
(3)在图1的基础上,以棱AB为轴将容器向左或向右旋转,但不能使液体溢出.图3或图4是其正面示意图,若液面与棱C′C或CB交于点P、点Q始终在棱BB′上,设PC=x,BQ=y,分别就图3和图4求y与x的函数关系式,并写出相应的α的范围.

分析 (1)根据水面与水平面平行可以得到CQ与BE平行,利用勾股定理即可求得BQ的长;
(2)液体正好是一个以△BCQ是底面的直棱柱,据此即可求得液体的体积;
(3)根据液体体积不变,当0°≤α≤37°时,列方程$\frac{1}{2}$(x+y)×4×4=24和当37°<α≤53°时,列方程$\frac{1}{2}$×y×(4-x)×4=24,求解即可.
解答 解:(1)∵液体的形状为直三棱柱,
∴CQ∥BE,
根据勾股定理得.BQ=$\sqrt{{5}^{2}-{4}^{2}}$=3;
在Rt△BCQ中,tan∠BCQ=$\frac{3}{4}$,
∴α=∠BCQ=37°.
故答案为CQ∥BE,3,37°.
(2)V液=$\frac{1}{2}$×3×4×4=24(dm3);
(3)当容器向左旋转时,0°≤α≤37°,
∵液体体积不变,
∴$\frac{1}{2}$(x+y)×4×4=24,
∴y=-x+3.
当容器向右旋转时,37°<α≤53°,
∵液体体积不变,
∴$\frac{1}{2}$×y×(4-x)×4=24,
∴y=$\frac{12}{4-x}$;
当液面恰好到达容器口沿,即点Q与点B′重合时,如图5,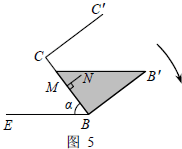
∵BB′=4,且$\frac{1}{2}$PB•BB′×4=24,
∴PB=3,
∴tan∠PB′B=$\frac{3}{4}$,
∴∠PB′B=37°.
∴α=∠B′PB=53°.
此时37°≤α≤53°;
点评 本题是几何变换综合题,主要考查了四边形的体积计算以及三视图的认识,正确理解棱柱的体积的计算是关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
14.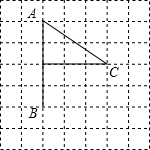 如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )
如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )
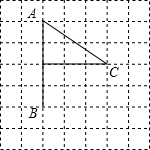 如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )
如图是幼儿园的李萌小朋友在方格纸上画出的小旗图案,若用(0,-1)表示点B,(0,3)表示A点,那么C点的位置可表示为( )| A. | (2,3) | B. | (1,3) | C. | (3,1) | D. | (3,0) |
12.若a3xby与-2a2ybx+1是同类项,则x+y=( )
| A. | 1 | B. | -1 | C. | -5 | D. | 5 |
14.单项式-$\frac{{a}^{2}b}{7}$的系数和次数分别是( )
| A. | -7,2 | B. | -$\frac{1}{7}$,2 | C. | -$\frac{1}{7}$,3 | D. | $\frac{1}{7}$,3 |