题目内容
16.已知函数y=(m2-4)x${\;}^{{m}^{2}-m-4}$+(m-3)x+2是二次函数,求它的解析式,并求出该二次函数的最大值或最小值.分析 直接利用二次函数的定义得出方程组,解方程组即可;利用配方法确定函数最值问题即可.
解答 解:由题意可得:$\left\{\begin{array}{l}{{m}^{2}-m-4=2}&{①}\\{{m}^{2}-4≠0}&{②}\end{array}\right.$,
由①得:m1=3,m2=-2
由②得:m≠2且m≠-2,
∴m=3,
∴y=5x2+2;
∵5>0,
∴x=0时,y有最大值2.
点评 本题考查二次函数的定义,最值问题,解题的关键是学会利用方程组解决问题,熟练掌握配方法确定函数最值问题,属于中考常考题型.

练习册系列答案
相关题目
20.下列各数中一定是负数的是( )
| A. | -a | B. | -a2 | C. | -a2+1 | D. | -a2-1 |
4.32015+5除以32012-1,所得的余数是( )
| A. | 313-1 | B. | 311-1 | C. | 32 | D. | 8 |
6.平面直角坐标系中,⊙O是以原点O为圆心,4为半径的圆,则点A(2,-2)的位置在( )
| A. | ⊙O内 | B. | ⊙O上 | C. | ⊙O外 | D. | 不能确定 |
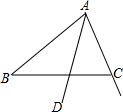 如图,在△ABC中,AB>AC,AD平分∠BAC
如图,在△ABC中,AB>AC,AD平分∠BAC