题目内容
 在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.
在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.(1)写出CG与EG的数量关系,并说明理由.
(2)若AD=12,AB=20,求CE的长.
考点:勾股定理,等腰三角形的判定与性质,直角三角形斜边上的中线,三角形中位线定理
专题:
分析:(1)利用直角三角形的性质以及等腰三角形的性质得出即可;
(2)首先得出EF
AD,进而得出ED,AD的长,再利用勾股定理得出EC的长.
(2)首先得出EF
| ∥ |
. |
| 1 |
| 2 |
解答: 解:(1)CG=EG,
解:(1)CG=EG,
理由:连接EG,∵AD⊥BC
∴∠ADB=90°
∵CE是AB边上的中线
∴E是AB的中点
∴DE=
AB(直角三角形斜边上的中线等于斜边的一半)
又∵AE=
AB
∴AE=DE
∵AE=CD
∴DE=CD
即△DCE是等腰三角形,
∵DG⊥EC,
∴CG=EG;
(2)过点E作EF⊥BC于点F,
∵AD⊥BC,E为AB的中点,
∴EF
AD,
∴EF=6,
∵∠ADB=90°,AD=12,AB=20,
∴BD=16,
∴FD=BF=8,
∴ED=
=10,
∴DC=10,
∴EC=
=
=6
.
 解:(1)CG=EG,
解:(1)CG=EG,理由:连接EG,∵AD⊥BC
∴∠ADB=90°
∵CE是AB边上的中线
∴E是AB的中点
∴DE=
| 1 |
| 2 |
又∵AE=
| 1 |
| 2 |
∴AE=DE
∵AE=CD
∴DE=CD
即△DCE是等腰三角形,
∵DG⊥EC,
∴CG=EG;
(2)过点E作EF⊥BC于点F,
∵AD⊥BC,E为AB的中点,
∴EF
| ∥ |
. |
| 1 |
| 2 |
∴EF=6,
∵∠ADB=90°,AD=12,AB=20,
∴BD=16,
∴FD=BF=8,
∴ED=
| 62+82 |
∴DC=10,
∴EC=
| EF2+FC2 |
| 62+(8+10)2 |
| 10 |
点评:此题主要考查了勾股定理以及三角形中位线的性质和等腰三角形的性质等知识,得出ED的长是解题关键.

练习册系列答案
相关题目
下列图形中,既是轴对称图形又是中心对称图形的是( )
| A、直角三角形 | B、等边三角形 |
| C、平行四边形 | D、正方形 |
圣诞节期间,某品牌圣诞树按成本价提高50%后标价,再打8折销售,利润为30元.设该圣诞树的成本价为x元,根据题意,下面所列方程正确的是( )
| A、(1+50%)x-x=30 |
| B、80%•(1+50%)x-x=30 |
| C、x-80%x=30 |
| D、50%x•80%=30 |
 有理数a、b、c在数轴上的位置如图所示,化简式子:|b|+|a-c|+|b-c|-|a-b|的值为:
有理数a、b、c在数轴上的位置如图所示,化简式子:|b|+|a-c|+|b-c|-|a-b|的值为: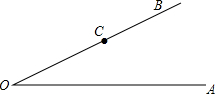 如图:点C是∠AOB的边OB上的一点,按下列要求画图并回答问题.
如图:点C是∠AOB的边OB上的一点,按下列要求画图并回答问题.