题目内容
1. 如图,已知在△ABC中,∠B>∠C,AD是BC边上的高,AE是∠BAC的平分线,求证:∠DAE=$\frac{1}{2}$(∠B-∠C).
如图,已知在△ABC中,∠B>∠C,AD是BC边上的高,AE是∠BAC的平分线,求证:∠DAE=$\frac{1}{2}$(∠B-∠C).
分析 根据三角形内角和定理以及AD是BC边上的高,求得∠BAD=90°-∠B,再根据AE平分∠BAC,求得∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C,最后根据∠DAE=∠BAE-∠BAD即可求解.
解答 证明:∵AD是BC边上的高,
∴∠BAD=90°-∠B.
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C.
∵∠DAE=∠BAE-∠BAD,
∴∠DAE=(90°-$\frac{1}{2}$∠B-$\frac{1}{2}$∠C)-(90°-∠B)=$\frac{1}{2}$∠B-$\frac{1}{2}$∠C=$\frac{1}{2}$(∠B-∠C).
点评 本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是三角形的内角和定理:三角形内角和是180°.

练习册系列答案
相关题目
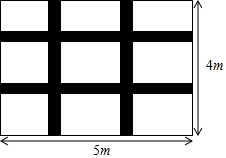 如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.求配色条纹的宽度.
如图,一块长5米宽4米的地毯,为了美观设计了两横、两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的$\frac{17}{80}$.求配色条纹的宽度.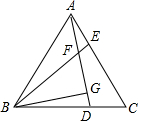 如图,等边三角形ABC中,D、E分别是BC、AC边上的两动点,且使BD=CE,BE与AD交于点F,BG⊥AD于点G,则$\frac{FG}{BF}$的值$\frac{1}{2}$.
如图,等边三角形ABC中,D、E分别是BC、AC边上的两动点,且使BD=CE,BE与AD交于点F,BG⊥AD于点G,则$\frac{FG}{BF}$的值$\frac{1}{2}$.