题目内容
3. 已知正方形ABCD,∠ADE=∠EAD=15°,求△BEC各内角度数.
已知正方形ABCD,∠ADE=∠EAD=15°,求△BEC各内角度数.
分析 如图,作辅助线;首先证明MD=CD;其次证明△MDE≌△CDE,得到ME=EC,进而证明BE=CE=MD=DC=BC,即可解决问题.
解答  解:如图,过点E作EF⊥AD于点F;作∠ADM=60°,
解:如图,过点E作EF⊥AD于点F;作∠ADM=60°,
则∠MDE=75°;而∠ADE=∠EAD=15°,
∴AE=DE,EF平分∠AED,AF=DF;
∴∠DEM=$\frac{180°-2×15°}{2}$=75°,
∴∠M=180°-2×75°=30°,∠MED=∠MDE=75°
∴DM=2DF,MD=ME;而DC=AD=2DF,
∴MD=CD;在△MDE与△CDE中,
$\left\{\begin{array}{l}{MD=CD}\\{∠MDE=∠CDE}\\{DE=DE}\end{array}\right.$,
∴△MDE≌△CDE(SAS),
∴ME=EC;同理可证ME=BE;
∴BE=CE=MD=DC=BC,
∴△BEC为等边三角形,
∴△BEC各内角度数为60°.
点评 该题主要考查了正方形的性质、全等三角形的判定及其性质等几何知识点及其应用问题;解题的关键是作辅助线,灵活运用正方形的性质、全等三角形的判定及其性质等几何知识点来分析、判断、解答.

练习册系列答案
相关题目
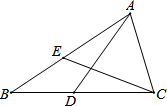 如图,△ABC中,点D在BC上,点E在AB上,BD=BE,要使△ADB≌△CEB,还需添加一个条件.
如图,△ABC中,点D在BC上,点E在AB上,BD=BE,要使△ADB≌△CEB,还需添加一个条件.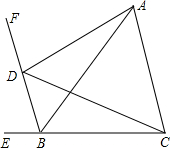 已知,BF平分△ABC的外角ABE,D为BF上一动点.
已知,BF平分△ABC的外角ABE,D为BF上一动点.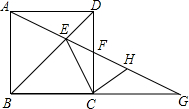 已知正方形ABCD,直线AG分别交BD、CD于点E、F,交BC的延长线于点G,点H是线段FG上的点,且HC⊥CE,求证:点H是GF的中点.
已知正方形ABCD,直线AG分别交BD、CD于点E、F,交BC的延长线于点G,点H是线段FG上的点,且HC⊥CE,求证:点H是GF的中点. 在等腰直角△ABC中,∠ACB=90°,D是AC中点,∠ADF=∠CDB,连接CF交BD于E,求证:BD⊥CF.
在等腰直角△ABC中,∠ACB=90°,D是AC中点,∠ADF=∠CDB,连接CF交BD于E,求证:BD⊥CF.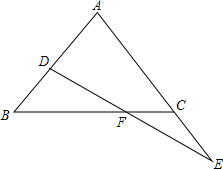 如图,在△ABC中,AB=AC,D是AB上一点,E是AC延长线上一点,且CE=BD,连结DE交BC于F.
如图,在△ABC中,AB=AC,D是AB上一点,E是AC延长线上一点,且CE=BD,连结DE交BC于F.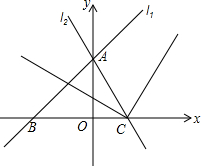 如图,平面直角坐标系中,直线l1:y=x+$\sqrt{3}$交x轴于B,交y轴于A,直线l2过点A交x轴正半轴于点C,并且OC:OB=1:$\sqrt{3}$,射线CE、CF分别为∠ACB及其外角的平分线.点M、N同时从A点出发,沿射线AB、AC方向运动.点M的运动速度为每秒$\sqrt{6}$个单位长度,点N的运动速度为每秒2个单位长度.直线MN与射线CE、CF交于点E、F,设运动时间为t秒.
如图,平面直角坐标系中,直线l1:y=x+$\sqrt{3}$交x轴于B,交y轴于A,直线l2过点A交x轴正半轴于点C,并且OC:OB=1:$\sqrt{3}$,射线CE、CF分别为∠ACB及其外角的平分线.点M、N同时从A点出发,沿射线AB、AC方向运动.点M的运动速度为每秒$\sqrt{6}$个单位长度,点N的运动速度为每秒2个单位长度.直线MN与射线CE、CF交于点E、F,设运动时间为t秒.