题目内容
【题目】如图,AB为⊙O的直径 ,点C在⊙O上,过点O作![]() 交BC于点E,交⊙O于点D,CD∥AB.
交BC于点E,交⊙O于点D,CD∥AB.
(1)求证:E为OD的中点;
(2)若CB=6,求四边形CAOD的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)由垂径定理得![]() ,由两直线平行,内错角相等,得
,由两直线平行,内错角相等,得![]() ,由角边角可证得
,由角边角可证得![]() 与
与![]() ,由全等三角形的对应边相等,即可得证;
,由全等三角形的对应边相等,即可得证;
(2)连接![]() ,由直径所对的圆周角是
,由直径所对的圆周角是![]() °,得
°,得![]() °,由垂径定理,得∴
°,由垂径定理,得∴![]() =
= ![]() ,
,
![]() ∥
∥![]() ,所以四边形
,所以四边形![]() 是平行四边形,由线段垂直平分线的性质可得
是平行四边形,由线段垂直平分线的性质可得![]() ,可证
,可证![]() 是等边三角形,
是等边三角形, ![]() °.在
°.在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
, ![]() .由此,
.由此, ![]() ,可得四边形CAOD的面积为
,可得四边形CAOD的面积为![]() .
.
试题解析:(1)∵在⊙O中, ![]() 于
于![]() ,
,
∴![]() ,
,
∵CD∥AB,
∴![]() .
.
在![]() 与
与![]() 中,
中, 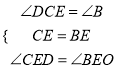 ,
,
∴![]() ≌
≌![]()
∴![]() ,
,
∴![]() 为
为![]() 的中点;
的中点;
(2)连接![]() ,
,
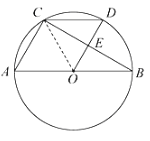
∵![]() 是⊙O的直径,
是⊙O的直径,
∴![]() °,
°,
∵![]() ,
,
∴![]() °=
°= ![]() ,
,
∴![]() ∥
∥![]() ,
,
∵![]() ∥
∥![]() ,
,
∴四边形![]() 是平行四边形
是平行四边形
∵![]() 是
是![]() 的中点,
的中点, ![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() °,
°,
∴![]() °
°![]() °,
°,
∴在![]() 中,
中, ![]() .
.
∵![]()
∴![]() .
.
∵![]() ,
,
∴![]() ,
, ![]() .
.
∴![]()
∴![]() .
.

练习册系列答案
相关题目