Question

【题目】如图，在正方形ABCD中，E是BC的中点，F是CD上一点，AE⊥EF．有下列结论：①∠BAE＝∠EAF；②射线FE是∠AFC的角平分线；③CF＝CD；④AF＝AB+CF．其中正确结论的个数为（　　）

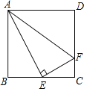
A.1个B.2个C.3个D.4个

Answer 1

【答案】D

【解析】

①设正方形的边长为2,然后求出AE、FC、EF，然后比较正切函数值即可；

②由已知条件，可得∠AEB和∠CFE的正切值，从而可以得到射线FE是否为∠AFC的角平分线；

④结合②③的结论，确定CF和CD的关系，从而可以判断CF=CD是否成立；

④由已知条件和全等三角形的判定与性质以及线段的和差即可判定AF=AB+CF是否成立．

解：设正方形的边长为2

∵在正方形ABCD中， E是BC的中点

∴AB=BC=2，BE=EC=AB=1，∠C=∠B=90°，

∴AE=,tan∠BAE=

∵∠BAE+∠AEB=90°，∠AEB+∠BAE =90°，

∴∠BAE=∠BAE

∴tan∠FEC=,CE=1

∴CF=

∴EF=

∴tan∠EAF =

∴∠BAE＝∠EAF，故①正确；

∴tan∠CFE=，tan∠AFE=，

∴∠AFE=∠CFE，即射线FE是∠AFC的角平分线，故②正确；

∵BC=CD，BC=2CE=4CF，

∴CF=CD，故③正确；

作EG⊥AF于点G，

∵FE平分∠AFC，∠C=90°，

∴EG=EC，

∴EG=EB，

∵∠B=∠AGE=90°，

在Rt△ABE和Rt△AGE中

AE=AE，EB=EG

∴Rt△ABE≌Rt△AGE（HL）

∴AB=AG，

又∵CF=GF，AF=AG+GF，

∴AF=AB+CF，故④正确；

综上共有4个正确结论．

故答案为D．