题目内容
15.【新知理解】如图①,若点A、B在直线l同侧,在直线l上找一点P,使AP+BP的值最小.
作法:作点A关于直线l的对称点A',连接A'B交直线l于点P,则点P即为所求.
【解决问题】
如图②,AD是边长为6cm的等边三角形ABC的中线,点P、E分别在AD、AC上,则PC+PE的最小值为3$\sqrt{3}$cm;
【拓展研究】
如图③,在四边形ABCD的对角线AC上找一点P,使∠APB=∠APD.(保留作图痕迹,并对作图方法进行说明)
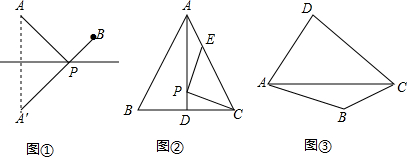
分析 (1)作点E关于AD的对称点F,连接PF,则PE=PF,根据两点之间线段最短以及垂线段最短,得出当CF⊥AB时,PC+PE=PC+PF=CF(最短),最后根据勾股定理,求得CF的长即可得出PC+PE的最小值;
(2)根据轴对称的性质进行作图.方法1:作B关于AC的对称点E,连接DE并延长,交AC于P,连接BP,则∠APB=∠APD.方法2:作点D关于AC的对称点D',连接D'B并延长与AC的交于点P,连接DP,则∠APB=∠APD.
解答 解:(1)【解决问题】
如图②,作点E关于AD的对称点F,连接PF,则PE=PF,
当点F,P,C在一条直线上时,PC+PE=PC+PF=CF(最短),
当CF⊥AB时,CF最短,此时BF=$\frac{1}{2}$AB=3(cm),
∴Rt△BCF中,CF=$\sqrt{B{C}^{2}-B{F}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$(cm),
∴PC+PE的最小值为3$\sqrt{3}$cm,
故答案为:3$\sqrt{3}$;
(2)【拓展研究】
方法1:如图③,作B关于AC的对称点E,连接DE并延长,交AC于P,点P即为所求,连接BP,则∠APB=∠APD.
方法2:如图④,作点D关于AC的对称点D',连接D'B并延长与AC的交于点P,点P即为所求,连接DP,则∠APB=∠APD.
点评 本题属于轴对称-最短路线问题,本题考查了勾股定理、轴对称的性质,利用轴对称作图与基本作图等知识点的综合应用,熟知两点之间,线段最短以及垂线段最短是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.下列各组数中,数值相等的是( )
| A. | 34和43 | B. | -42和(-4)2 | C. | -23和(-2)3 | D. | (-2×3)3和23×33 |
7.下列各数中:+(-5)、|-1-2|、-$\frac{π}{2}$、-(-7)、0、(-2015)3,负数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
5. 某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:
某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:
某校60名学生体育测试成绩成绩统计表
(说明:40-55分为不合格,55-70分为合格,70-85分为良好,85-100分为优秀)
请根据以上信息,解答下列问题:
(1)表中的a=18;b=0.5;c=3;d=0.05.
(2)请根据频数分布表,画出相应的频数分布直方图.
 某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:
某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩成绩统计表
| 成绩 | 划记 | 频数 | 频率 |
| 优秀 | 正正正 | a | 0.3 |
| 良好 | 正正正正正正 | 30 | b |
| 合格 | 正 | 9 | 0.15 |
| 不合格 |   | c | d |
| 合计 |
请根据以上信息,解答下列问题:
(1)表中的a=18;b=0.5;c=3;d=0.05.
(2)请根据频数分布表,画出相应的频数分布直方图.
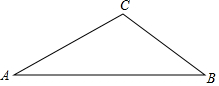 如图,在△ABC中,∠A=30°,cosB=$\frac{4}{5}$,AC=6$\sqrt{3}$.求AB的长.
如图,在△ABC中,∠A=30°,cosB=$\frac{4}{5}$,AC=6$\sqrt{3}$.求AB的长. 如图,利用标杆BE测量建筑物DC的高度,如果标杆BE长为1.5米,测得AB=2米,BC=8米,且点A、E、D在一条直线上,则楼高CD是7.5米.
如图,利用标杆BE测量建筑物DC的高度,如果标杆BE长为1.5米,测得AB=2米,BC=8米,且点A、E、D在一条直线上,则楼高CD是7.5米.