题目内容
4.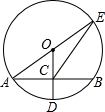 如图⊙O中,半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC,若AB=8,CD=10,则EC的长度为( )
如图⊙O中,半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC,若AB=8,CD=10,则EC的长度为( )| A. | 2$\sqrt{5}$ | B. | 8 | C. | 2$\sqrt{10}$ | D. | 2$\sqrt{13}$ |
分析 连结BE,设⊙O的半径为R,由OD⊥AB,根据垂径定理得AC=BC=$\frac{1}{2}$AB,在Rt△AOC中,OA=R,OC=R-CD=R-2,根据勾股定理得到(R-2)2+42=R2,解得R=5,则OC=3,由于OC为△ABE的中位线,则BE=2OC=6,再根据圆周角定理得到∠ABE=90°,然后在Rt△BCE中利用勾股定理可计算出CE的长.
解答  解:连结BE,设⊙O的半径为R,如图,
解:连结BE,设⊙O的半径为R,如图,
∵OD⊥AB,
∴AC=BC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,
在Rt△AOC中,OA=R,OC=R-CD=R-10,
∵OC2+AC2=OA2,
∴(R-10)2+42=R2,解得R=5,
∴OC=5-2=3,
∴BE=2OC=6,
∵AE为直径,
∴∠ABE=90°,
在Rt△BCE中,CE=$\sqrt{B{C}^{2}+B{E}^{2}}$=2$\sqrt{13}$.
故选D.
点评 本题考查了垂径定理、勾股定理、圆周角定理的运用,熟记和圆有关的基本性质是解题的关键.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
14.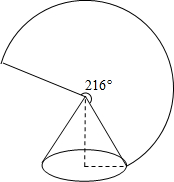 如图所示,圆锥的母线长为10cm,其侧面展开图是圆心角为216°的扇形,则该圆锥的高为( )
如图所示,圆锥的母线长为10cm,其侧面展开图是圆心角为216°的扇形,则该圆锥的高为( )
 如图所示,圆锥的母线长为10cm,其侧面展开图是圆心角为216°的扇形,则该圆锥的高为( )
如图所示,圆锥的母线长为10cm,其侧面展开图是圆心角为216°的扇形,则该圆锥的高为( )| A. | 5cm | B. | 6cm | C. | 7cm | D. | 8cm |
15.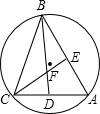 如图,△ABC内接于⊙O,∠A的度数为60°,∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E,CE、BD相交于点F.以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号数是( )
如图,△ABC内接于⊙O,∠A的度数为60°,∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E,CE、BD相交于点F.以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号数是( )
 如图,△ABC内接于⊙O,∠A的度数为60°,∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E,CE、BD相交于点F.以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号数是( )
如图,△ABC内接于⊙O,∠A的度数为60°,∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E,CE、BD相交于点F.以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号数是( )| A. | ①② | B. | ①③ | C. | ③④ | D. | ②④ |
12.$\sqrt{16}$的算术平方根是( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
19.下列计算结果正确的是( )
| A. | a3+a3=a6 | B. | a3•a2=a6 | C. | (a3)3=a9 | D. | a6÷a2=a3 |
9.下列各式从左到右变形正确的是( )
| A. | $\frac{x+1}{2}$+$\frac{y}{3}$=3(x+1)+2y | |
| B. | $\frac{0.2a-0.03b}{0.4c+0.05d}$=$\frac{2a-3b}{4c+5d}$ | |
| C. | $\frac{a-b}{b-c}$=$\frac{b-a}{c-b}$ | |
| D. | $\frac{2a-2b}{c+d}$=$\frac{a-b}{c+d}$ |
16.已知反比例函数y=$\frac{10}{x}$,当1<x<2时,y的取值范围是( )
| A. | y>10 | B. | 5<y<10 | C. | 1<y<2 | D. | 0<y<5 |
14.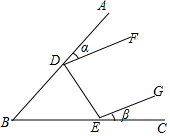 如图所示,点D,E分别在BA,BC上,∠ADF=α度,∠CEG=β度,∠ABC=γ度,DF∥EG,则( )
如图所示,点D,E分别在BA,BC上,∠ADF=α度,∠CEG=β度,∠ABC=γ度,DF∥EG,则( )
 如图所示,点D,E分别在BA,BC上,∠ADF=α度,∠CEG=β度,∠ABC=γ度,DF∥EG,则( )
如图所示,点D,E分别在BA,BC上,∠ADF=α度,∠CEG=β度,∠ABC=γ度,DF∥EG,则( )| A. | α+β+γ=180 | B. | α+β=γ | C. | α+β+γ=90 | D. | 2α+2β-γ=45 |
 碳纳米管可以看做是石墨烯片层卷曲而成,它的硬度与金刚石相当,拥有良好的柔韧性,因而被称为“超级纤维”,其构成方式主要由呈六边形排列的碳原子构成数层到数十层的同轴圆管,层与层之间的距离约0.34nm(1nm=0.000000001m),数据0.34nm用科学记数法可以表示为3.4×10-10m.
碳纳米管可以看做是石墨烯片层卷曲而成,它的硬度与金刚石相当,拥有良好的柔韧性,因而被称为“超级纤维”,其构成方式主要由呈六边形排列的碳原子构成数层到数十层的同轴圆管,层与层之间的距离约0.34nm(1nm=0.000000001m),数据0.34nm用科学记数法可以表示为3.4×10-10m.