题目内容
15.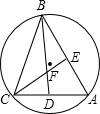 如图,△ABC内接于⊙O,∠A的度数为60°,∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E,CE、BD相交于点F.以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号数是( )
如图,△ABC内接于⊙O,∠A的度数为60°,∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E,CE、BD相交于点F.以下四个结论:①cos∠BFE=$\frac{1}{2}$;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号数是( )| A. | ①② | B. | ①③ | C. | ③④ | D. | ②④ |
分析 ①正确.只要证明∠BFE=60°即可;
②错误.利用反证法,假设成立.推出矛盾即可.
③正确.作FW⊥AC,FS⊥AB只要证明△FSE≌△WFD即可.
④错误.BF=DF是重心的性质,内心不一定成立.
解答 解:∵∠A=60°
∴∠ABC+∠BCA=180°-∠A=120°
∵∠ABC、∠ACB的角平分线分别是BD,CE
∴∠CBF+∠BCF=$\frac{1}{2}$(∠ABC+∠BCA)=60°=∠BFE
∴cos∠BFE=$\frac{1}{2}$,
∴即cos∠BFE=$\frac{1}{2}$;故①正确;
∵∠BDC=∠A+$\frac{1}{2}$∠ABC=60°+∠DBA
∠BCA=180°-∠A-2∠DBA=120°-2∠DBA
若BC=BD成立,则应有∠BDC=∠BCA
应有60°+∠DBA=120°-2∠DBA,
即∠DBA=20°,
此时∠ABC=40°,
∴∠BCD=∠BDC=80°,
而根据题意,没有条件可以说明∠ABC是40°,
故②错误;
∵点F是△ABC内心,作FW⊥AC,FS⊥AB
则FW=FS,∠FSE=∠FWD=90°∠EFD=∠SFW=120°
∴∠SFE=∠WFD,△FSE≌△WFD
∴FD=FE,故③正确;
由于点F是内心而不是各边中线的交点,故BF=2DF不一定成立,因此④不正确.
因此本题正确的结论为①③.
故选B.
点评 本题利用了三角形内角和定理,余弦的概念,角的平分线的性质,圆周角定理,全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考选择题中的压轴题.

练习册系列答案
相关题目
6.下列说法中正确的有( )
(1)两条直线被第三条直线所截,同位角相等;
(2)若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
(1)两条直线被第三条直线所截,同位角相等;
(2)若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余;
(3)相等的两个角是对顶角;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
3.若关于x的一元二次方程kx2-(2k+1)x+k+2=0,有两个不相等的实数根,则k的取值范围是( )
| A. | k≤$\frac{1}{4}$ | B. | k≤$\frac{1}{4}$且k≠0 | C. | k>$\frac{1}{4}$ | D. | k<$\frac{1}{4}$且k≠0 |
10.函数y=$\frac{1}{x+1}$中自变量x的取值范围是( )
| A. | x≥-1 | B. | x≤-1 | C. | x≠-1 | D. | x=-1 |
20. 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=70°,则∠1等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=70°,则∠1等于( )
 如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=70°,则∠1等于( )
如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=70°,则∠1等于( )| A. | 70° | B. | 100° | C. | 110° | D. | 80° |
4.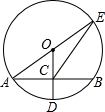 如图⊙O中,半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC,若AB=8,CD=10,则EC的长度为( )
如图⊙O中,半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC,若AB=8,CD=10,则EC的长度为( )
 如图⊙O中,半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC,若AB=8,CD=10,则EC的长度为( )
如图⊙O中,半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC,若AB=8,CD=10,则EC的长度为( )| A. | 2$\sqrt{5}$ | B. | 8 | C. | 2$\sqrt{10}$ | D. | 2$\sqrt{13}$ |
5.下列计算,正确的是( )
| A. | a3×a2=a6 | B. | a3÷a=a3 | C. | a2+a2=a4 | D. | (a2)2=a4 |
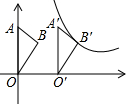 如图,在平面直角坐标系xOy中,点A在y轴上,点B的坐标为(1,2),将△AOB沿x轴向右平移得到△A′O′B′,点B的对应点B′恰好在函数y=$\frac{6}{x}$(x>0)的图象上,此时点A移动的距离为2.
如图,在平面直角坐标系xOy中,点A在y轴上,点B的坐标为(1,2),将△AOB沿x轴向右平移得到△A′O′B′,点B的对应点B′恰好在函数y=$\frac{6}{x}$(x>0)的图象上,此时点A移动的距离为2.