题目内容
如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
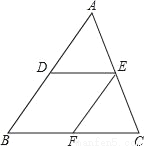
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
题目内容
如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.

(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?
 同步练习强化拓展系列答案
同步练习强化拓展系列答案