题目内容
7．若x2+mx+n分解因式的结果是（x+2）（x-1），则m+n=（ ）| A． | 1 | B． | -2 | C． | -1 | D． | 2 |
分析 根据因式分解的结果，利用多项式乘以多项式法则化简，再利用多项式相等的条件求出m与n的值，即可求出m+n的值．
解答 解：∵x2+mx+n=（x+2）（x-1）=x2+x-2，
∴m=1，n=-2，
则m+n=1-2=-1，
故选C
点评 此题考查了因式分解-十字相乘法，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
相关题目
18．经过矩形ABCD顶点A、D的圆与BC边相切，圆的半径为5，AD=8，则AB=（ ）
| A． | 22 | B． | 8 | C． | 2或8 | D． | 4或6 |
如图，某窗户由矩形和弓形组成，已知弓形的跨度AB=6m，弓形的高EF=2m，现设计安装玻璃，请帮工程师求出$\widehat{AB}$所在圆O的半径．
2．
如图放置一个水管三叉接头，则其俯视图是（ ）
如图放置一个水管三叉接头，则其俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
14．
如图，线段AB=4，C为线段AB上的一个动点，以AC、BC为边作等边△ACD和等边△BCE，⊙O外接于△CDE，则⊙O半径的最小值为（ ）
如图，线段AB=4，C为线段AB上的一个动点，以AC、BC为边作等边△ACD和等边△BCE，⊙O外接于△CDE，则⊙O半径的最小值为（ ）| A． | 4 | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\frac{3\sqrt{2}}{2}$ | D． | 2 |
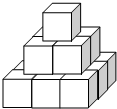如图，几个棱长为1的小正方体在地板上堆积成一个模型，表面喷涂红色染料，那么染有红色染料的模型的表面积为42．