题目内容
已知关于x的方程(k-1)x2+(2k-3)x+k+1=0有两个不相等的实数根,求实数k的取值范围.
考点:根的判别式
专题:
分析:方程(k-1)x2+(2k-3)x+k+1=0有两个不相等的实数根,可得△>0,再代入相应数值解不等式即可.
解答:解:由题意得:△=(2k-3)2-4×(k+1)(k-1)
=4k2-12k+9-4k2+4
=-12k+13>0,
解得:k<
且k≠1,
故实数k的取值范围为k<
且k≠1.
=4k2-12k+9-4k2+4
=-12k+13>0,
解得:k<
| 13 |
| 12 |
故实数k的取值范围为k<
| 13 |
| 12 |
点评:此题主要考查了根的判别式,关键是掌握一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
以下列长度的三条线段为边,能组成三角形的是( )
| A、3,2,5 |
| B、3,2,6 |
| C、3,3,5 |
| D、3,3,6 |
 如图,直线y=k1x+b与双曲线y=
如图,直线y=k1x+b与双曲线y= 如图,已知∠COB=4∠AOC,OD平分∠AOB,且∠COD=36°,求∠AOB的度数.
如图,已知∠COB=4∠AOC,OD平分∠AOB,且∠COD=36°,求∠AOB的度数.
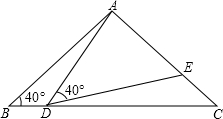 如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E. 如图,∠AOB=38°,∠BOC=96°,OD是∠AOC的平分线,求∠BOD的度数?
如图,∠AOB=38°,∠BOC=96°,OD是∠AOC的平分线,求∠BOD的度数? 如图所示,已知边长分别为a,b的两个正方形并排放着,则阴影部分的面积为多少?
如图所示,已知边长分别为a,b的两个正方形并排放着,则阴影部分的面积为多少?