题目内容
已知:如图等腰直角△ABC和△ECD中,∠ACB=∠ECD=90°,AC=BC,EC=DC.

(1)求证:BE=AD;
(2)若将△ECD绕点C逆时针方向旋转一个锐角,并延长BE交AD于点F,交AC于点O.求证:BF⊥AD;
(3)在②的条件下,取BE的中点M,取AD的中点N,求∠MNC的度数.

(1)求证:BE=AD;
(2)若将△ECD绕点C逆时针方向旋转一个锐角,并延长BE交AD于点F,交AC于点O.求证:BF⊥AD;
(3)在②的条件下,取BE的中点M,取AD的中点N,求∠MNC的度数.
考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:(1)利用“边角边”证明△BEC和△ACD全等,再根据全等三角形对应边相等可得BE=AD;
(2)先求出∠BCE=∠ACD,再利用“边角边”证明△BEC和△ACD全等,再根据全等三角形对应角相等可得∠CBE=∠CAD,然后求出∠AFB=∠ACB=90°,然后根据垂直的定义证明即可;
(3)连接MC,根据全等三角形对应角相等可得∠CBE=∠CAD,全等三角形对应边相等可得AD=BE,然后求出BM=AN,再利用“边角边”证明△BMC和△ANC全等,根据全等三角形对应边相等可得CM=CN,全等三角形对应角相等可得∠BCM=∠ACN,再求出∠MCN=∠ACB=90°,判断出△MCN是等腰直角三角形,再根据等腰直角三角形的性质解答.
(2)先求出∠BCE=∠ACD,再利用“边角边”证明△BEC和△ACD全等,再根据全等三角形对应角相等可得∠CBE=∠CAD,然后求出∠AFB=∠ACB=90°,然后根据垂直的定义证明即可;
(3)连接MC,根据全等三角形对应角相等可得∠CBE=∠CAD,全等三角形对应边相等可得AD=BE,然后求出BM=AN,再利用“边角边”证明△BMC和△ANC全等,根据全等三角形对应边相等可得CM=CN,全等三角形对应角相等可得∠BCM=∠ACN,再求出∠MCN=∠ACB=90°,判断出△MCN是等腰直角三角形,再根据等腰直角三角形的性质解答.
解答:(1)证明:在△BEC和△ACD中,
,
∴△BEC≌△ACD(SAS),
∴BE=AD;
(2)∵∠ACB=∠ECD=90°,
∴∠ACB-∠ACE=∠ECD-∠ACE,
即∠BCE=∠ACD,
在△BEC和△ACD中,
,
∴△BEC≌△ACD(SAS),
∴∠CBE=∠CAD,
∴∠AFB=∠ACB=90°,
∴BF⊥AD;
(3)如图,连接MC,∵△BEC≌△ACD,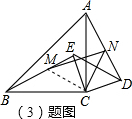
∴∠CBE=∠CAD,AD=BE,
∵M是BE的中点,N是AD的中点,
∴BM=AN,
在△BMC和△ANC中,
,
∴△BMC≌△ANC(SAS),
∴CM=CN,∠BCM=∠ACN,
∴∠MCN=∠ACB=90°,
∴△MCN是等腰直角三角形,
∴∠MNC=45°.
|
∴△BEC≌△ACD(SAS),
∴BE=AD;
(2)∵∠ACB=∠ECD=90°,
∴∠ACB-∠ACE=∠ECD-∠ACE,
即∠BCE=∠ACD,
在△BEC和△ACD中,
|
∴△BEC≌△ACD(SAS),
∴∠CBE=∠CAD,
∴∠AFB=∠ACB=90°,
∴BF⊥AD;
(3)如图,连接MC,∵△BEC≌△ACD,

∴∠CBE=∠CAD,AD=BE,
∵M是BE的中点,N是AD的中点,
∴BM=AN,
在△BMC和△ANC中,
|
∴△BMC≌△ANC(SAS),
∴CM=CN,∠BCM=∠ACN,
∴∠MCN=∠ACB=90°,
∴△MCN是等腰直角三角形,
∴∠MNC=45°.
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,熟练掌握各性质与三角形全等的判定方法并准确识图是解题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图所示,直线MN与△ABC的外接圆相切于点A,AC平分∠MAB,如果AN=6,
如图所示,直线MN与△ABC的外接圆相切于点A,AC平分∠MAB,如果AN=6, 如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AC、ED的中点,连接DO并延长到点E,使OE=OD,连接AE,CE.
如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AC、ED的中点,连接DO并延长到点E,使OE=OD,连接AE,CE.

