��Ŀ����
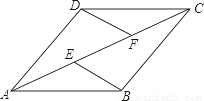
��ͼ����֪AD�ǡ�O��ֱ����BC�ǡ�O���ң�AD��BC������Ϊ��E��AE=BC=16�����O��ֱ����

��ϰ��ϵ�д�
 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
�����Ŀ
У���������10˫�˶�Ь�ij���ͳ�������
���루cm�� | 25 | 25.5 | 26 | 26.5 | 27 |
��������˫�� | 1 | 1 | 2 | 4 | 2 |
����10˫�˶�Ь�������������λ���ֱ�Ϊ��������
A. 4cm��26cm B. 4cm��26.5cm
C. 26.5cm��26.5cm D. 26.5cm��26cm
C ������������λ��Ҫ�����ݴ�С�����˳�����У�λ�����м��һ����������������ƽ������Ϊ��λ����������һ�������г��ִ����������ݣ�ע���������Բ�ֹһ��. �������� ����һ��������26.5�dz��ִ������ģ���������26.5cm�� �������������м�λ�õ�����26.5��26.5����ô��λ���Ķ����֪���������ݵ���ֱ��˽�ǣ�26.5+26.5����2=26.6cm. ��ѡC. ...

 ��
��
 n��n��3����
n��n��3���� n��n��3��=20 ��
n��n��3��=20 ��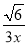 B. y=x2+x C. y=
B. y=x2+x C. y=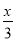 D. y=4x+8
D. y=4x+8