题目内容
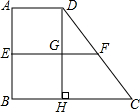 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=1,BC=3,CD=4,梯形的高DH与中位线EF交于点G,则下列结论中:
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,AD=1,BC=3,CD=4,梯形的高DH与中位线EF交于点G,则下列结论中:①△DGF≌△EBH;②S△DGF:S△DHC=1:4;③四边形EHCF是菱形;④以CD为直径的圆与AB相切于点E,
其中正确的有
考点:四边形综合题
专题:综合题
分析:根据梯形的性质和DH为梯形的高得到BH=AD=1,则CH=BC-BH=2,再根据梯形的中位线性质得EF∥CH,EF=2,即有EF=CH,于是可判断四边形EHCF为平行四边形,加上CH=CF=2,于是可判断四边形EHCF为菱形;根据菱形的性质得EH=CF=DF,再利用GF为△DHC的中位线得GF=1,所以BH=GF,则可根据“HL”证明Rt△DGF≌Rt△EBH;利用GF∥CH可判断△DGF∽△DHC,根据相似的性质得
=
;由EF∥BC,AB⊥BC得到EF⊥AB,再根据EF=2,CD=4,F点为CD的中点得到EF是以CD为直径的圆的半径,于是根据切线的判定定理可判断以CD为直径的圆与AB相切于点E.
| S△DGF |
| S△DHC |
| 1 |
| 4 |
解答:解:∵AD∥BC,AB⊥BC,DH为梯形的高,
∴BH=AD=1,
∴CH=BC-BH=3-1=2,
∵EF为梯形的中位线,
∴EF∥CH,EF=
(AD+BC)=2,
∴EF=CH,
∴四边形EHCF为平行四边形,
而F点为CD的中点,
∴DF=CF=
CD=2,
∴CH=CF,
∴四边形EHCF为菱形,所以③正确;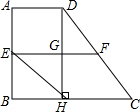
∴EH=CF=DF,
∵GF为△DHC的中位线,
∴GF=
CH=1,
∴BH=GF,
在Rt△DGF和Rt△EBH中
,
∴Rt△DGF≌Rt△EBH,所以①正确;
∵GF∥CH,
∴△DGF∽△DHC,
∴
=(
)2=(
)2=
,所以②正确;
∵EF∥BC,AB⊥BC,
∴EF⊥AB,
∵EF=2,CD=4,
而F点为CD的中点,
∴EF是以CD为直径的圆的半径,
∴以CD为直径的圆与AB相切于点E,所以④正确.
故答案为①②③④.
∴BH=AD=1,
∴CH=BC-BH=3-1=2,
∵EF为梯形的中位线,
∴EF∥CH,EF=
| 1 |
| 2 |
∴EF=CH,
∴四边形EHCF为平行四边形,
而F点为CD的中点,
∴DF=CF=
| 1 |
| 2 |
∴CH=CF,
∴四边形EHCF为菱形,所以③正确;

∴EH=CF=DF,
∵GF为△DHC的中位线,
∴GF=
| 1 |
| 2 |
∴BH=GF,
在Rt△DGF和Rt△EBH中
|
∴Rt△DGF≌Rt△EBH,所以①正确;
∵GF∥CH,
∴△DGF∽△DHC,
∴
| S△DGF |
| S△DHC |
| GF |
| CH |
| 1 |
| 2 |
| 1 |
| 4 |
∵EF∥BC,AB⊥BC,
∴EF⊥AB,
∵EF=2,CD=4,
而F点为CD的中点,
∴EF是以CD为直径的圆的半径,
∴以CD为直径的圆与AB相切于点E,所以④正确.
故答案为①②③④.
点评:本题考查了四边形的综合题:熟练掌握梯形的性质、梯形的中位线性质和菱形的判定与性质;会利用“HL”证明直角三角形全等;会运用相似三角形的判定与性质以及圆的切线的判定定理.

练习册系列答案
相关题目
式子
在实数范围内有意义,则x的取值范围是( )
| 2-x |
| A、x≥-2 | B、x≥2 |
| C、x≤-2 | D、x≤2 |
下列命题的逆命题是假命题的是( )
| A、两直线平行,同位角相等 |
| B、两直线平行,内错角相等 |
| C、两三角形全等,三对对应边相等 |
| D、两三角形全等,三对对应角相等 |
 …
… ”,在前16个图案中有
”,在前16个图案中有 ”,在前2014个图案中有
”,在前2014个图案中有 ”.
”. 如图是一组密码的一部分,为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),则可发现“努”的坐标与其有一定的关系,根据其关系,破译“正做数学”的真实意思是
如图是一组密码的一部分,为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.若“今”所处的位置为(x,y),则可发现“努”的坐标与其有一定的关系,根据其关系,破译“正做数学”的真实意思是 如图,是一直角三角板,线段AB>AC的数学道理是
如图,是一直角三角板,线段AB>AC的数学道理是