题目内容
18.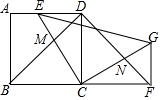 如图,正方形ABCD,点E在AD上,将△CDE绕点C顺时针旋转90°至△CFG,点F,G分别为点D,E旋转后的对应点,连接EG,DB,DF,DB与CE交于点M,DF与CG交于点N.
如图,正方形ABCD,点E在AD上,将△CDE绕点C顺时针旋转90°至△CFG,点F,G分别为点D,E旋转后的对应点,连接EG,DB,DF,DB与CE交于点M,DF与CG交于点N.(1)求证BM=DN;
(2)直接写出图中已经存在的所有等腰直角三角形.
分析 (1)根据正方形的性质得∠DCB=90°,CD=CB,再根据旋转的性质得CF=CD,∠ECG=∠DCF=90°,则可判断△CDF为等腰直角三角形,所以∠CDF=∠CFD=45°,然后证明△BCM≌△DCN,则BM=DN;
(2)根据正方形的性质可判断△ABD和△BCD为等腰直角三角形,根据旋转的性质可判断△CDF和△ECG为等腰直角三角形,然后判断△BDF为腰直角三角形.
解答 (1)证明:∵四边形ABCD为正方形,
∴∠DCB=90°,CD=CB,
∵△CDE绕点C顺时针旋转90°至△CFG,
∴CF=CD,∠ECG=∠DCF=90°,
∴△CDF为等腰直角三角形,
∴∠CDF=∠CFD=45°,
∵∠BCM+∠DCE=90°,∠DCN+∠DCE=90°,
∴∠BCM=∠DCN,
∵∠CBM=$\frac{1}{2}$∠ABC=45°,
∴∠CBM=∠CDN,
在△BCM和△DCN中
$\left\{\begin{array}{l}{∠MBC=∠NDC}\\{CB=CD}\\{∠BCM=∠CDN}\end{array}\right.$,
∴△BCM≌△DCN,
∴BM=DN;
(2)解:∵四边形ABCD为正方形,
∴△ABD和△BCD为等腰直角三角形;
由(1)得△CDF为等腰三角形;
∵△CDE绕点C顺时针旋转90°至△CFG,
∴CE=CG,∠ECG=90°,
∴△ECG为等腰直角三角形;
∵△CBD和△CFD为等腰直角三角形;
∴△BDF为等腰直角三角形.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的判定方法和正方形的性质.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
8.已知P(a,3)和Q(4,b)关于x轴对称,则(a+b)2016的值为( )
| A. | 1 | B. | -1 | C. | 72016 | D. | -72016 |
9.下面各组的两个比不能组成比例的是( )
| A. | 8:7和16:14 | B. | 0.6:0.2和3:1 | C. | 19:110和10:9 | D. | 0.2:1.2和$\frac{2}{5}$:2.4 |
 如图,用吸管吸易拉罐内的饮料时,吸管与易拉罐的上、下底面所形成的角分别是∠1和∠2,若∠1=110°,则∠2=70°.(易拉罐的上下底面互相平行)
如图,用吸管吸易拉罐内的饮料时,吸管与易拉罐的上、下底面所形成的角分别是∠1和∠2,若∠1=110°,则∠2=70°.(易拉罐的上下底面互相平行)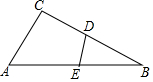 如图,在△ABC中,点D是BC边上的动点(不与点B、C重合),点E是AB边上的动点(不与点A、B重合),则当满足条件∠A=∠BDE(答案不唯一)时,△ABC与△DEB相似(写出一个即可).
如图,在△ABC中,点D是BC边上的动点(不与点B、C重合),点E是AB边上的动点(不与点A、B重合),则当满足条件∠A=∠BDE(答案不唯一)时,△ABC与△DEB相似(写出一个即可).