题目内容
 已知,如图,BD=CD,BE⊥AC于点E,CF⊥AB于F.
已知,如图,BD=CD,BE⊥AC于点E,CF⊥AB于F.求证:AD是∠BAC的角平分线.
分析:利用“角角边”证明△BDF和△CDE全等,根据全等三角形对应边相等可得DE=DF,再根据到角的两边距离相等的点在角的平分线上证明.
解答:证明:在△BDF和△CDE中,
,
∴△BDF≌△CDE(AAS),
∴DE=DF,
又∵BE⊥AC,CF⊥AB,
∴AD是∠BAC的角平分线.
|
∴△BDF≌△CDE(AAS),
∴DE=DF,
又∵BE⊥AC,CF⊥AB,
∴AD是∠BAC的角平分线.
点评:本题考查了全等三角形的判定与性质,到角的两边距离相等的点在角的平分线上,熟记三角形全等的判定方法和角平分线的判定是解题的关键.

练习册系列答案
相关题目
 已知:如图,BD是AC边上的高,DE⊥BC于E,BE:EC=5:1.若AD=2,AB=8.
已知:如图,BD是AC边上的高,DE⊥BC于E,BE:EC=5:1.若AD=2,AB=8.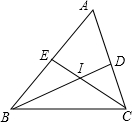 已知:如图,BD平分∠ABC,CE平分∠ACE,BD与CE交于点I,试说明∠BIC=90°+
已知:如图,BD平分∠ABC,CE平分∠ACE,BD与CE交于点I,试说明∠BIC=90°+ 22、已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.试说明:PM=PN.
22、已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.试说明:PM=PN.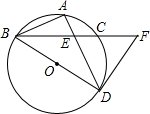 已知:如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连接AB.
已知:如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连接AB. 已知:如图,BD、CE是△ABC的两条高,M是BC的中点.求证:ME=MD.
已知:如图,BD、CE是△ABC的两条高,M是BC的中点.求证:ME=MD.