题目内容
10.现有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字-1,2,5,;乙袋中装有3个完全相同的小球,分别标有数字3,-5,-7;小宇从甲袋中随机摸出一个小球,记下数字为m,小惠从乙袋中随机摸出一个小球,记下的数字为n.(1)若点Q的坐标为(m,n),求点Q在第四象限的概率;
(2)已知关于x的一元二次方程2x2+mx+n=0,求该方程有实数根的概率.
分析 (1)首先根据题意列表,然后根据表格求得所有等可能的结果与摸出的两个球上数字横坐标大于0,纵坐标小于0的可能情况,再利用概率公式求解即可;
(2)若一元二次方程2x2+mx+n=0,则其跟的判别式大于等于0,进而可求出该方程有实数根的概率.
解答 解:(1)
| -1 | 2 | 5 | |
| 3 | (-1,3) | (2,3) | (5,3) |
| -5 | (-1,-5) | (2,-5) | (5,-5) |
| -7 | (-1,-7) | (2,-7) | (5,-7) |
(2)∵关于x的一元二次方程2x2+mx+n=0方程有实数根,
∴△≥0,
即m2-8n≥0,
∴m2≥8n,
由(1)可知满足条件的m,n组合共7对,
∴该方程有实数根的概率=$\frac{7}{9}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
18.某树苗培育基地培育了1000棵银杏树苗,为了解树苗的长势,测量了6棵树苗的高(单位:cm),其分别为51,48,51,49,52,49,则这1000棵树苗的方差的估计值为( )
| A. | 1 | B. | 1.5 | C. | 2 | D. | 3 |
5.2015年4月30日,苏州吴江蚕种全部发放完毕,共计发放蚕种6460张(每张上的蚕卵有200粒左右),涉及6个镇,各镇随即开始孵化蚕种,小李所记录的蚕种孵化情况如表所示,则可以估计蚕种孵化成功的概率为( )
| 累计蚕种孵化总数/粒 | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 |
| 孵化成功数/粒 | 181 | 362 | 541 | 718 | 905 | 1077 | 1263 |
| A. | 0.95 | B. | 0.9 | C. | 0.85 | D. | 0.8 |
19.下列方程中解为x=2的是( )
| A. | 3x+(10-x)=20 | B. | 4(x+0.5)+x=7 | C. | x=-$\frac{1}{2}$x+3 | D. | $\frac{1}{7}$(x+14)=$\frac{1}{4}$(x+20) |
20.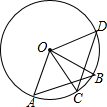 如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )
如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )
 如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )
如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )| A. | AC=BD | B. | AC<BD | C. | AC>BD | D. | 不确定 |

 如图,小明用长为3m的竹竿CD做测量共计,测量学校旗杆AB的高度,移动竹竿,使O、C、A在同一直线上,此时OD=6m,DB=12m,则旗杆AB的高为9m.
如图,小明用长为3m的竹竿CD做测量共计,测量学校旗杆AB的高度,移动竹竿,使O、C、A在同一直线上,此时OD=6m,DB=12m,则旗杆AB的高为9m.