题目内容
已知多项式(2x2+ax-y+6)-(2bx2-3x+5y-1)
(1)若多项式的值与字母x的值无关,求a,b的值;
(2)在(1)的条件下,求多项式3(a2-2ab-b2)-(3a2+ab+b2)的值;
(3)在(1)的条件下,求 (b+a2)+(2b+
•a2)+(3b+
•a2)+…+(2013b+
•a2)的值.
(1)若多项式的值与字母x的值无关,求a,b的值;
(2)在(1)的条件下,求多项式3(a2-2ab-b2)-(3a2+ab+b2)的值;
(3)在(1)的条件下,求 (b+a2)+(2b+
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2012×2013 |
考点:整式的加减,整式的加减—化简求值
专题:
分析:(1)已知多项式相减列出关系式,去括号合并得到最简结果,根据结果与x无关求出a与b的值;
(2)把a、b的值代入整理后的代数式;
(3)将a与b的值代入原式变形,计算即可得到结果.
(2)把a、b的值代入整理后的代数式;
(3)将a与b的值代入原式变形,计算即可得到结果.
解答:解:(1)(2x2+ax-y+6)-(2bx2-3x+5y-1)=2(1-b)x2+(a-3)x-6y+7.
∵该多项式的值与字母x的值无关,
∴1-b=0,a+3=0,
解得:a=-3,b=1;
(2)由(1)知,a=-3,b=1.
则3(a2-2ab-b2)-(3a2+ab+b2),
=-3ab-2b2
=-3×(-3)×1-2×12
=9-2
=7;
(3)将a=-3,b=1代入得:
原式=(1+2+…+2013)+(1+1-
+
-
+…+
-
)×2013
=
+(1+1-
)×2013
=2031116.
∵该多项式的值与字母x的值无关,
∴1-b=0,a+3=0,
解得:a=-3,b=1;
(2)由(1)知,a=-3,b=1.
则3(a2-2ab-b2)-(3a2+ab+b2),
=-3ab-2b2
=-3×(-3)×1-2×12
=9-2
=7;
(3)将a=-3,b=1代入得:
原式=(1+2+…+2013)+(1+1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2012 |
| 1 |
| 2013 |
=
| 2013×(1+2013) |
| 2 |
| 1 |
| 2013 |
=2031116.
点评:此题考查了整式的加减,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若⊙O1、⊙O2的直径分别为4和6,圆心距O1O2=2,则⊙O1与⊙O2的位置关系是( )
| A、相交 | B、外离 | C、外切 | D、内切 |
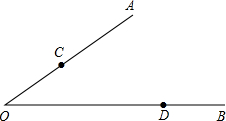 画图:如图,已知点C、点D分别在∠AOB的边上,请根据下列语句画出图形:
画图:如图,已知点C、点D分别在∠AOB的边上,请根据下列语句画出图形: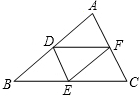 如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,求证:△ABC∽△DEF.
如图,在△ABC中,点D、E、F分别是AB、BC、CA的中点,求证:△ABC∽△DEF.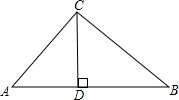 如图,已知在△ABC中,CD⊥AB于D,且BC2=BD•AB,判断△ABC的形状,并说明理由.
如图,已知在△ABC中,CD⊥AB于D,且BC2=BD•AB,判断△ABC的形状,并说明理由. 如图,已知C点为线段AB的中点,D点为BC的中点,AB=4cm,求AD的长度.
如图,已知C点为线段AB的中点,D点为BC的中点,AB=4cm,求AD的长度.