题目内容
3．已知直线y=kx+b，若k+b=-$\sqrt{15}$，kb=$\sqrt{2}$-1，那么该直线不经过第一象限．分析 首先根据k+b=-$\sqrt{15}$，kb=$\sqrt{2}$-1确定k、b的符号，然后根据一次函数的性质确定其不经过的象限即可．
解答 解：∵直线y=kx+b，k+b=-$\sqrt{15}$，kb=$\sqrt{2}$-1，
∴k＜0，b＜0，
∴图象呈下降趋势，且交y轴于负半轴，
∴不经过第一象限，
故答案为：一．
点评 本题考查了一次函数的图象与系数的关系，解题的关键是能够根据提供的k、b的关系确定k、b的符号，难度不大．
练习册系列答案
相关题目
13．用火柴棒按下列方式搭建三角形：
（1）填表：
（2）当三角形的个数为n时，火柴棒的根数是多少？（用含n的式子表示）
（3）求当n=100时，火柴棒的根数是多少？
（4）当火柴棒的根数为2013时，三角形的个数是多少？
（1）填表：
| 三角形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 3 | 5 | 7 | 9 | 11 |
（3）求当n=100时，火柴棒的根数是多少？
（4）当火柴棒的根数为2013时，三角形的个数是多少？
11．
如图，?OABC的顶点C在x轴的正半轴上，顶点A、B在第一象限内，且点A的横坐标为2，对角线AC与OB交于点D，若反比例函数y=$\frac{10}{x}$的图象经过点A与点D，则?OABC的面积为（ ）
如图，?OABC的顶点C在x轴的正半轴上，顶点A、B在第一象限内，且点A的横坐标为2，对角线AC与OB交于点D，若反比例函数y=$\frac{10}{x}$的图象经过点A与点D，则?OABC的面积为（ ）| A． | 30 | B． | 24 | C． | 20 | D． | 16 |
18．
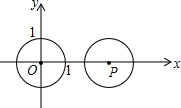如图，平面直角坐标系中，⊙O半径长为1，点P在x轴上，⊙P的半径长为2，把⊙P向左平移，当⊙P与⊙O相切时，点P的横坐标的值为（ ）
如图，平面直角坐标系中，⊙O半径长为1，点P在x轴上，⊙P的半径长为2，把⊙P向左平移，当⊙P与⊙O相切时，点P的横坐标的值为（ ）| A． | 3 | B． | 1 | C． | 1，3 | D． | ±1，±3 |
8．下列运算正确的是（ ）
| A． | -3-2=-1 | B． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C． | a6÷a3=a3 | D． | （a+b）2=a2+b2 |
15．
如图，直线l1∥l2，∠2=65°，∠3=60°，则∠1为（ ）
如图，直线l1∥l2，∠2=65°，∠3=60°，则∠1为（ ）| A． | 65° | B． | 60° | C． | 55° | D． | 50° |
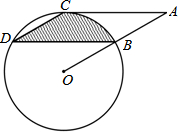如图，点B，C，D都在⊙O上，过点C作AC∥BD交OB延长线于点A，连接CD，且∠CDB=∠OBD=30°，BD=4$\sqrt{3}$，则由弦CD，BD与弧BC所围成的阴影部分的面积是$\frac{8}{3}$π．（结果保留π）