题目内容
3.(1)化简:$\frac{{a}^{2}+4a}{(a+2)(a-2)}$-$\frac{a-2}{{a}^{2}-4}$+a选一个你喜欢的a值,代入并求值.(2)解方程:$\frac{1}{6x-2}$=$\frac{1}{2}$-$\frac{2}{1-3x}$.
分析 (1)先进行同分母的减法运算,再把分子分解因式,然后约分得到原式=$\frac{a+1}{a-2}$,再把满足条件的a的值代入计算即可;
(2)先把方程两边都乘以2(3x-1)得到整式方程,然后解整式方程后进行检验即可得到原方程的解.
解答 解:(1)原式=$\frac{{a}^{2}+4a}{(a+2)(a-2)}$-$\frac{a-2}{(a+2)(a-2)}$
=$\frac{{a}^{2}+4a-a+2}{(a+2)(a-2)}$
=$\frac{(a+2)(a+1)}{(a+2)(a-2)}$
=$\frac{a+1}{a-2}$,
当a=0时,原式=$\frac{0+1}{0-2}$=-$\frac{1}{2}$;
(2)去分母1=3x-1+4,
解得x=-$\frac{2}{3}$,
检验:当x=-$\frac{2}{3}$时,2(3x-1)≠0,x=-$\frac{2}{3}$是原方程的解,
所以原方程的解为x=-$\frac{2}{3}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也考查了解分式方程.

练习册系列答案
相关题目
18.下列图形中既是中心对称图形,又是轴对称的图形是( )
| A. | 平等四边形 | B. | 等边三角形 | C. | 正五边形 | D. | 正方形 |
8.下列各式中不能用平方差公式分解的是( )
| A. | -16a2+b2 | B. | -a4-b2 | C. | $\frac{1}{225}$-m4 | D. | x2-81y2 |
13.已知a-b=1,则代数式2a-2b+2013的值是( )
| A. | 2015 | B. | 2014 | C. | 2012 | D. | 2011 |
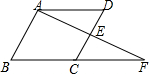 如图,在?ABCD中,过点A作AB的垂线恰好经过DC的中点E,且交BC的延长线于点F,已知AB=4cm,∠B=60°,则该平行四边形的周长是16cm.
如图,在?ABCD中,过点A作AB的垂线恰好经过DC的中点E,且交BC的延长线于点F,已知AB=4cm,∠B=60°,则该平行四边形的周长是16cm.