题目内容
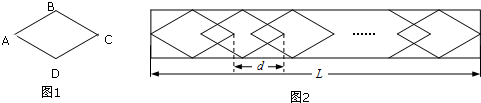
18.某工厂沿路护栏纹饰部分是由若干个和菱形ABCD(图1)全等的图案组成的,每增加一个菱形,纹饰长度就增加dcm,如图2所示.已知菱形ABCD的边长6$\sqrt{3}$cm,∠BAD=60°.(1)求AC长;
(2)若d=15,纹饰总长度L为3918cm,则需要多少个这样的菱形图案?
分析 (1)连接AC,BD,设交点为O,根据菱形的性质以及勾股定理即可求出AO的长,进而可求出AC的长;
(2)设需要x个这样的图案,仍然根据L=菱形对角线的长+(x-1)d进行计算即可
解答 解:
(1)连接AC,BD,设交点为O,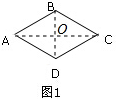
∵四边形ABCD是菱形,∠BAD=60°,
∴∠DAC=30°,
∴OD=$\frac{1}{2}$AD=3$\sqrt{3}$,
∴OA=$\sqrt{A{D}^{2}-O{D}^{2}}$=9,
则AC=2OA=18;
(2)当d=15时,设需x个菱形图案,则有:18+15×(x-1)=3918,
解得x=261,
即需要261个这样的菱形图案.
点评 本题考查了菱形的性质,解直角三角形的应用,此题主要考查学生能否能根据图形找出规律,题目比较好,有一定的难度.

练习册系列答案
相关题目
9.某市一周空气质量报告某项污染指数的数据是:31,35,31,33,30,33,31.则对于这列数据表述正确的是( )
| A. | 众数是30 | B. | 中位数是31 | C. | 平均数是33 | D. | 极差是35 |
6.下列命题中,假命题的是( )
| A. | 两条直线平行,同位角相等 | B. | 对顶角相等 | ||
| C. | 同位角相等 | D. | 直角都相等 |
13.已知关于x、y的方程组$\left\{\begin{array}{l}{y-x=m-1}\\{2y+x=m+1}\end{array}\right.$的解x、y满足3x+y≥0,求m的取值范围.
10.下列命题中逆命题错误的是( )
| A. | 内错角相等两直线平行 | B. | 直角三角形的两锐角互余 | ||
| C. | 全等三角形的对应边相等 | D. | 互为相反数的两个数的绝对值相等 |
7.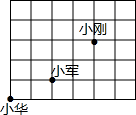 课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )
 课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )
课间操时,小华、小军、小刚的位置如图所示,小军对小刚说,如果我的位置用(-1,0)表示,小华的位置用(-3,-1)表示,那么你的位置可以表示成( )| A. | (1,2) | B. | (1,3) | C. | (0,2) | D. | (2,2) |
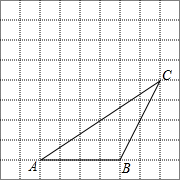 如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个长度单位.
如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个长度单位.