题目内容
函数y=x2+bx+c与y=bx+c在同一坐标系中的图象大致是
- A.

- B.

- C.

- D.

C
分析:根据A、B、C、D图中直线的性质,求出b、c的符号,再根据b、c的符号判断二次函数的图象是否符合题意.
解答:A、∵直线过一、二、三象限,∴b>0,c>0,根据二次函数的图象,c<0,故本选项错误;
B、∵直线过二、三、四象限,∴b<0,c<0,根据二次函数的图象,抛物线的对称轴为x=- <0,
<0,
则b>0,故本选项错误;
C、∵直线过二、三、四象限,∴b<0,c<0,根据二次函数的图象,抛物线的对称轴为x=- >0,
>0,
则b<0,c<0,故本选项正确;
D、∵直线过一、三、四象限,∴b>0,c<0,根据二次函数的图象,抛物线的对称轴为x=- >0,
>0,
则b<0,c<0,故本选项错误.
故选C.
点评:本题考查了二次函数的图象与一次函数的图象在同一坐标系中的共存问题,分别分析两个函数图象,得到矛盾的结论是解答此类题目的基本思路.
分析:根据A、B、C、D图中直线的性质,求出b、c的符号,再根据b、c的符号判断二次函数的图象是否符合题意.
解答:A、∵直线过一、二、三象限,∴b>0,c>0,根据二次函数的图象,c<0,故本选项错误;
B、∵直线过二、三、四象限,∴b<0,c<0,根据二次函数的图象,抛物线的对称轴为x=-
 <0,
<0,则b>0,故本选项错误;
C、∵直线过二、三、四象限,∴b<0,c<0,根据二次函数的图象,抛物线的对称轴为x=-
 >0,
>0,则b<0,c<0,故本选项正确;
D、∵直线过一、三、四象限,∴b>0,c<0,根据二次函数的图象,抛物线的对称轴为x=-
 >0,
>0,则b<0,c<0,故本选项错误.
故选C.
点评:本题考查了二次函数的图象与一次函数的图象在同一坐标系中的共存问题,分别分析两个函数图象,得到矛盾的结论是解答此类题目的基本思路.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知二次函数y=x2-bx+1(-1<b<1),在b从-1变化到1的过程中,它所对应的抛物线的位置也随之变化,下列关于抛物线的移动方向描述正确的是( )
| A、先往左上方移动,再往左下方移动 | B、先往左下方移动,再往左上方移动 | C、先往右上方移动,再往右下方移动 | D、先往右下方移动,再往右上方移动 |
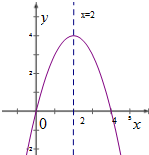 二次函数y=-x2+bx+c的图象如图所示,下列几个结论:
二次函数y=-x2+bx+c的图象如图所示,下列几个结论: