题目内容
7．
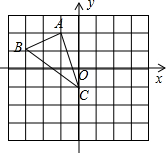如图，图形中每一小格正方形的边长为1，已知△ABC．（1）AC的长等于$\sqrt{10}$，△ABC的面积等于3.5．
（2）先将△ABC向右平移2个单位得到△A′B′C′，则A点的对应点A′的坐标是（1，2）．
（3）再将△ABC绕点C按逆时针方向旋转90°后得到△A1B1C1，则A点对应点A1的坐标是（-3，-2）．
分析 （1）利用勾股定理即可求解；
（2）A的坐标是（-1，2），向右平移2个单位长度，则A′的坐标即可写出；
（3）根据旋转的性质，即可求解．
解答 
解：（1）AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
S△ABC=3×3-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×3=3.5，
故答案为：$\sqrt{10}$；3.5；
（2）A点的对应点A′的坐标是（1，2），
故答案为：（1，2）．
（3）并写出A点对应点A1的坐标是（-3，-2）．
故答案为：（-3，-2）．
点评 本题主要考查了旋转及平移变换，解题的关键是旋转及平移变换的变化特征．
练习册系列答案
相关题目
18．小明是“环保小卫士”，课后他经常关心环境天气的变化，他了解到本周白天的平均气温，如表（“+”表示比前一天上升了，“-”表示比前一天下降了．单位：℃）
已知上周周日平均气温是16.9℃，回答下列问题：
（1）这一周哪天的平均气温最高，最高是多少？
（2）计算这一周每天的平均气温．
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 气温变化 | +1.1 | -0.3 | +0.2 | +0.4 | +1 | +1.4 | -0.3 |
（1）这一周哪天的平均气温最高，最高是多少？
（2）计算这一周每天的平均气温．
如图，在△ABC中，AC=6cm，AB=9cm，D是边BC上一点，AD平分∠BAC，在AB上截取AE=AC，连结DE，已知DE=2cm，BD=3cm．求：